正十二面体と黄金比（その１：面心図から）

・正十二面体の直投影
　先月の記事で，黄金比と正五角形の関係について述べた。その正五角形からなる正多面体である正十二面体も，黄金比と密接な関係がある。今回から三回かけて，正十二面体の直投影を通して，正十二面体と黄金比の関係について触れてみたい。
　多面体の直投影については，前々回ざっと説明したが，大事なことを確認しておく。
　直投影とは，平行光線による，それと垂直なスクリーンへの投影である。よって，多面体上の，スクリーンに平行な多角形や線分は，それと合同な多角形や線分に投影される。多面体上の，互いに平行な線分は，互いに平行な線分に投影され，しかもそれらの線分の長さの比は等しい。つまり平行性と長さの比は保たれる。線分上に内分点があれば，それを直投影しても，内分比は変わらない。
　正十二面体は正五角形の面のみで構成されている。よって，正十二面体の直投影は，正五角形を直投影した五角形のみで構成される。一般の配置では，正十二面体の面はスクリーンと平行でないため，直投影の五角形は正五角形ではない。正五角形ではないが，正五角形と同様に黄金比を多くもつ五角形である。

　このことは，直投影が平行線分の長さの比を変えないことからわかる。この五角形の各辺には，それぞれ平行な対角線がある。平行な辺と対角線の長さの比は黄金比 $\phi$ である。また，各々の対角線は，他の対角線を黄金分割する。一本の対角線は，五角形の高さを黄金分割し，五角形の面積を黄金二乗分割する。さらに，対角線を引いてできる三角形*1の面積は５種類あり，それらを順に並べると隣合う面積の比は黄金比 $\phi$ になっている。

・正十二面体の面心直投影
　正十二面体の対向面の中心をつなぐ直線は，五回対称軸である。すなわち，この軸まわりに，360°/5＝72°回転させると正十二面体は回転前と完全に一致する。よって，この軸に平行な光線で直投影をおこなうと，その投影図は五回対称性をもつ。
　中心に一つの正五角形面があり，これはもとの正十二面体の面と合同である。よって正十二面体の稜長を１とすると，投影図の中央の正五角形の辺長も１である。これを下方の図では赤線で示した。

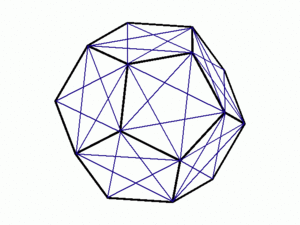
　この正五角形の各頂点から放射状に線分が伸び，それらの先端が少し大きな正五角形（水色）の頂点の位置に来る。そしてここから二本づつ線分が伸びて，投影図の輪郭は正十角形になっている。輪郭が正十角形になる理由は，対称性からというだけで充分であろう。隠線を描けば一目瞭然だ（右図）。

・面心直投影図の寸法
　正十二面体の面心図では，面は中心に１枚，周囲に５枚の計６枚見えている。正十角形の大きさはどれくらいだろうか？これは簡単に求めることができる。先の大きな正五角形に注目すると，これは中心の正五角形と相似比が黄金比 $\phi$ になっている。なぜなら，大きな正五角形の辺は，周辺５枚の五角形の対角線であり，この対角線（水色）の長さはこれと平行な辺（赤）の長さの $\phi$ 倍だからである。これさえわかれば，作図が可能になる。

　寸法をいくつか求めておこう。まず， $AB=1$ ， $CE=\phi\simeq1.618$
$OA=\frac{GA}{\sin{\frac{\pi}{5}}}=\frac{\frac{1}{2}}{\sin{\frac{\pi}{5}}}=\frac{1}{\sqrt{3-\phi}}\simeq0.851$
$OE=OD={\phi}OA=\frac{\phi}{\sqrt{3-\phi}}\simeq1.376$
$OG=\frac{GA}{\tan{\frac{\pi}{5}}}=\frac{\frac{1}{2}}{\tan{\frac{\pi}{5}}}=\frac{\phi}{2\sqrt{3-\phi}}\simeq0.688$
　上２式から，GはODの中点であるから，ABとODはGにおいて互いを垂直二等分する。よって，△AODは底角36°の二等辺三角形。すると，△DAEは△ODEと相似な黄金三角形*2であることがわかり，二等辺三角形であるから，DE=DA=OA。つまり，輪郭の正十角形の辺長は，中央の正五角形の外接円半径と一致する。
　次に黄色の線に着目して，周辺の五角形がどの程度つぶれているかを調べる。
$GH=GO+OH=GO+OA=GO+\frac{2}{\phi}GO=(1+2\phi-2)GO=(2\phi-1)GO$
GO=GDであったから，中央の正五角形と周辺の五角形は，底辺を共有して高さの比が $(2\phi-1):1=$ 約2.236:1になっている。当然，面積比も $(2\phi-1):1$ で，輪郭の正十角形の面積*3は，中央の正五角形の $1+\frac{5}{2\phi-1}=2\phi=$ 約3.236倍である。

・二面角の算出
　面心図に現れる二種の五角形の寸法から，正十二面体の二面角δを求めることができる。
　中心の正五角形に投影される面は光線と垂直，スクリーンと平行であり，周辺のつぶれた五角形に投影される面がスクリーンとなす角はδの補角である。そして面がスクリーンとなす角は，その法線が光線となす角と等しく，これをθとすると，その面の直投影はもとの面を一方向にcosθだけ縮小した形になる。そしてすぐ上で見たように，面心図において，つぶれた五角形は正五角形を対称軸の方向に $(2\phi-1)$ 分の1に縮小したものであるから，
$\cos(\pi-\delta)=2\phi-1=\sqrt{5}$ 　であり，これを解くと，二面角δは約116.6°となる。

・正十角形からの作図
　正十二面体の面心直投影は，正十角形から次のようにして簡単に作図できる。

１．正十角形に，頂点を二つおきにつなぐ対角線を描く。対角線は星型正十角形*4になる。
２．対角線の芯にできる正十角形の頂点を一つおきにつないで，正五角形を描く。
３．正五角形の頂点と輪郭の正十角形の頂点を，放射状につなぐ。
４．隠線もまったく同様にして得られる。