ジタバグと正多面体
・直交三長方形の凸包
前回の記事で,中心で直交する3枚の長方形の頂点をつないで得られる多面体について触れた。凸多面体としては,一般には二十面体で,黄金長方形のときに正二十面体,長方形が正方形のときは立方八面体,長方形が線分に退化したときは正八面体が得られるのであった。
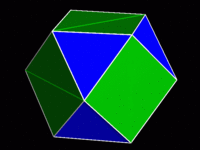


前回のCGでは,3枚の長方形を変形させるときに,長方形の対角線の長さを保つように変形させていた。そのため,多面体の各面の大きさは,変形にともなって変化している。今回は,多面体を構成する8枚の正三角形の大きさが不変になるようにした(上図)。多面体の変形にともない,残りの12枚の二等辺三角形は,変形するものの,その等辺の長さは一定である。
・バッキーのジタバグ
ここで,正三角形の面だけ残して二等辺三角形の面を消してみる。すると多面体は,8枚の正三角形が,頂点同士で相互につながった穴あきの形状になる。それぞれの穴を2枚の二等辺三角形で塞げば,もとの多面体が復元できる。



これは次のような模型で実現できる。24本の等長な棒を,立方八面体の稜を構成するようにつなぎあわせる。棒のつなぎ目は,関節のように自由に回転できるようにしておく。すると,正三角形を囲む3本の棒は,相互に動くことができないが,正方形を囲む4本の棒は自由度があって動ける。これによって,模型を変形させることができ,それにともなって正方形の部分が変形する。辺の長さが一定なので,正方形は「菱形」に変形するが,この「菱形」は平面上になく,対角線で折れ曲がって三次元空間に飛び出している。
正三角形の部分は変形しないので,面を貼ってもいい。CGでは,稜のみにすると形状がつかみにくいので,そうせざるを得ないが,実際に模型をつくる場合は面がなくてもいい。この模型は,バックミンスター・フラーが「ジタバグ(Jitterbug)」と名付けたものである。フラーは二十世紀に活躍したアメリカの建築家で,フラードーム(測地線ドーム)やバッキーボール(フラーレン)にも名を残す有名人だ。
立方八面体の状態から,穴の正方形を変形して,対向する頂点が稜の長さと等しい距離に近づいたとき,ジタバグは正二十面体の枠になっている。さらに変形して,対向する頂点間の距離がゼロになったとき,ジタバグは正八面体そのものになっている。この様子を動画にしてみた。
ジタバッグ.gif ![]()
・黄金二乗長方形と正十二面体
この推移において,正二十面体と正八面体の間に,正十二面体と関係の深い状態がある。四角形の穴の対向頂点間距離と,稜長の比が黄金比になったとき,ジタバグは正十二面体に内接するのだ。ジタバグの12個の頂点が,外接正十二面体の頂点に一致する。正十二面体の頂点は全部で20個あるが,残りの8個は,ジタバグの正三角形の中心の上方にある。



なお,穴の対向頂点は2組あって,各組で頂点間距離は異なるが,ジタバグが正二十面体に内接するとき,いづれの頂点間距離も,稜長との比が黄金比になっている。すなわち,
近接頂点距離:稜長:遠隔頂点距離 となっている。
これは次のように言い換えられる。直交三長方形の凸包は,正三角形8枚,二等辺三角形12枚からなる二十面体であるが,二等辺三角形が黄金三角形になるとき,二十面体は正十二面体に内接する。このとき,12枚の黄金三角形は正十二面体の各面に現れる大きな黄金三角形と一致している。もとになる長方形は,短辺と長辺の長さの比がである。いわば,黄金二乗長方形だ。
結局,中心で直交する3枚の黄金二乗長方形の凸包は,正三角形8枚,黄金三角形12枚からなる二十面体であり,正十二面体に内接する。この二十面体と正十二面体は,12個の頂点が一致し,正十二面体の残りの8頂点は,立方体の頂点と一致する。この立方体は,もとの黄金二乗長方形と同心で,立方体の稜長は,黄金二乗長方形の長短どちらの辺の長さとも黄金比になっている。つまり,
長方形短辺の長さ:立方体の稜長:長方形長辺の長さ となっている。
・ジタバグと正多面体
ジタバグは,8枚の正三角形からなるが,正八面体の状態からさらに畳んでいくと,面が重なって正四面体を作ることもできる。そして,立方八面体の形態において,ジタバグは立方体に内接する。このとき,ジタバグの12頂点は立方体の稜の中点に一致し,立方体の面がジタバグの穴をぴったり塞ぐような配置になる。
結局,ジタバグは,最も大きな立方八面体の状態から,どんどん小さく畳んでいくことによって,5つの正多面体すべてを経由する。立方体→正二十面体→正十二面体→正八面体→正四面体の順である。





正四面体を除く4つの正多面体は,変形する直交三長方形の凸包から出てくる。凸包は,長方形が正方形のとき立方体に内接し,黄金長方形のとき正二十面体と一致し,黄金二乗長方形のとき正十二面体に内接し,長方形が線分に退化するとき正八面体と一致する。
| 凸包 | 立方体に内接*1 | 正二十面体 | 正十二面体に内接 | 正八面体 |
|---|---|---|---|---|
| 直交三長方形 | 正方形 | 黄金長方形 | 黄金二乗長方形 | 線分 |
| 二等辺三角形 | 直角二等辺三角形*2 | 正三角形 | 黄金三角形 | 線分 |