正多面体の投影図

・投影法
　コンピュータのディスプレイも，紙の上も，縦横二次元の世界である。だから，そこに三次元図形を描くには，どうしても二次元の図形として描かなくてはならない。三次元図形を二次元図形に変換するのだが，このときにもっとも普通に行われる方法が投影法である。
　つまり，三次元空間内に，光源と，三次元図形と，スクリーンとしての平面を，この順で並ぶように配置し，スクリーン上に物体の影ができるようにして，映ったその影を求める二次元図形（投影図）とするのである。多面体をスクリーンに投影する様子を描いた図を掲げる。光源を白丸で示してある。
　このとき，多面体を不透明なものにしてしまうと，投影像は単なる中実の多角形になってしまい，多面体としての構造が皆目わからない*1。よって通常は，投影される多面体として，稜のみからなるフレームモデルを使用する。ただし，そのままでは稜同士の重なり具合が表現できず，立体感がなくなるため，光源から見て裏側に位置する稜の像を，点線や細線で弱々しく描いたり，又はまったく描かない，という隠線処理をする。

・直投影
　投影法には，光源の位置，形，スクリーンと光源との関係などによって，さまざまなものがあり，図学の教科書には網羅的な説明が載っている。中でも特に重要なのが，直投影と透視投影である。下に，立方体を直投影した図を示す。

　直投影とは，無限遠にある光源などによって平行光線をつくり，その光線と直交するようにスクリーンを配置して得られる投影である。直投影によると，スクリーンに平行な図形（多角形や線分）の投影像は，もとの図形と形もサイズも等しい合同な図形になる。スクリーンに平行でない線分は，直投影によって長さが変わる（短くなる）が，互いに平行な複数の線分は，直投影によってその長さの比を変えない。つまり，平行で等長な線分は，平行で等長な線分に投影される（このことは上図でも確認できる）。
　直投影において，線分とその像の長さの比は，それがスクリーンとなす角度θのみによって決まる。具体的にはこの比はcosθであり，スクリーンとの距離によらない。よって，直投影では遠近感が得られず，投影図はのっぺりした感じになる。直投影は，すべての光線がスクリーンと直交すればよいので，光源の位置を無限遠とするかわりに，光源をスクリーンに平行な無限平面としてもよい。

・透視投影
　これに対して，透視投影では，実際の見た目に近い，遠近感のある投影図が得られる。透視投影では，光源は点光源であり，スクリーンから有限の距離にある。初めに掲げた正二十面体の投影の様子は透視投影のものであった。立体上の点と，スクリーン上にできるその点の像を結ぶ直線は，一点（光源）で交わる。この関係は，人間が物体を見たり，カメラで物体を撮影する場合とまったく同様である。物体表面から出た光は，次第に収束して一点で交わった後再び拡がって，網膜上，又はフィルム上に像を結ぶ*2。

　上図左は立方体の透視投影の様子，右図は得られた投影図である。直投影とは異なり，平行な４本の稜の像が平行になっていないことがわかる。このように，透視投影では，互いに平行な線分が平行な線分に投影されない。互いに平行な線分の像は，延長するとある一点で交わり*3，これを消失点という。線分の長さの比も保たれない。そのため，透視投影図の描き方はなかなか煩雑である。

・正多面体の直投影
　直投影は，平行な線分の長さの比を保ち，スクリーンに平行な線分の長さを不変にするのであった。そのため，直投影図は比較的容易に作図することができる。逆に言うと，直投影では，多面体の寸法の情報を正確に表現することができ，これは幾何学的な考察にはとても都合がよい。以下では，特に正多面体の直投影について述べていく。
　直投影では，光線はスクリーンに垂直であるが，立体をどのような向きで配置するかによって，得られる投影像が異なってくる。正多面体においては，面心直投影，稜心直投影，点心直投影がよく使われる。これらは，正多面体の中心と，面の中心，稜の中点，頂点をそれぞれ結ぶ直線が，光線と平行になるような配置から得られる直投影である。面心直投影では，正多面体の面がスクリーンと平行，稜心直投影では，稜がスクリーンと平行になる。これら三種の直投影では，光線が正多面体の対称軸と平行になっているのがポイントであり，得られる投影図は，その対称軸の対称性と同等の対称性を備えている。

・正四面体
　正四面体の面心直投影は，構成面と合同な正三角形になる。隠線を描くなら，それは正三角形の中心と頂点を結ぶ線分になる。稜心直投影は，正方形に対角線を描き込んだものになる。一方の対角線は隠線である。点心直投影は，正三角形に，中心と頂点を結ぶ線分を加えたものである。面心，稜心，点心の各投影によって，正四面体の三回対称軸，二回対称軸，三回対称軸が中心の一点に投影される。それに応じて，面心図，稜心図，点心図は，それぞれ三回，二回，三回対称性をもっている。隠線を区別しなければ，稜心図は四回対称性を獲得する。

・立方体
　立方体の面心直投影は，正方形である。稜心直投影は，白銀長方形*4に，長辺の中点をつなぐ線分を描き込んだものになる。点心直投影は，正六角形に，中心と頂点を結ぶ線分を書き加えたもので，これらの線分を一つおきに選んだものは隠線である。面心図，稜心図，点心図は，それぞれ四回，二回，三回対称性をもつ。隠線を区別しなければ，点心図は六回対称性を獲得する。

・正八面体
　正八面体の面心直投影は，同心で逆さの正三角形を組み合わせたダビデの星に，六つの頂点をつないだ正六角形を加えたものになる。一方の正三角形の辺は隠線である。稜心直投影は，白銀菱形*5に，短い対角線を加えたものになり，点心直投影は，正方形に対角線を加えたものになる。面心図，稜心図，点心図は，それぞれ三回，二回，四回対称性をもつ。隠線を区別しなければ，面心図は六回対称性を獲得する。正八面体は立方体と双対であり，同一の回転対称性をもつから，一方の面心図と他方の点心図の対称性は等しく，両者の稜心図の対称性は等しい。

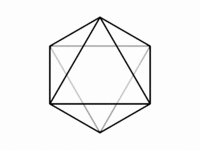
・正十二面体，正二十面体
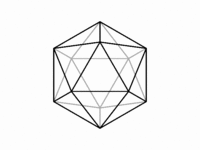
　互いに双対な正十二面体と正二十面体の直投影は，次に掲げるようなものになる。正十二面体の面心図，稜心図，点心図は，それぞれ五回，二回，三回対称性をもつ。隠線を区別しなければ，面心図は十回対称性を獲得し，点心図は六回対称性を獲得する。正二十面体の直投影についての対称性は，面心図と点心図を入れ替えたものである。

*1:図では面を半透明にしている。

*2:実際には，眼やカメラには，水晶体やレンズがあるので，文字通りの直線ではないが，光にとっての直線は光線であり，物体上の点と，網膜上にできるその点の像を結ぶ光線は，一点で交わっている。レンズのないピンホールカメラであれば，物体上の点と，フィルム上にできるその点の像を結ぶ直線は，文句なしに一点で交わる。

*3:互いに平行な線分がスクリーンにも平行な場合は，線分の像も互いに平行であり，消失点はできない。この場合も線分の長さの比は保たれない。

*4:長辺の長さが短辺の長さの√２倍の長方形。√２は白銀比と呼ばれる。

*5:長い対角線の長さが短い対角線の長さの√２倍である菱形。