正八面体の爆縮
・正八面体の爆発
正八面体は，各面を底面とする８個の合同な正三角錐に分割することができる。これらの正三角錐は，頭頂点がすべて正八面体の中心に集まっている。この状態から，正三角錐をまっすぐ外へ移動させていくと，正八面体が８個の破片になって飛んでゆくように見える。いわば正八面体の爆発である。
爆発８.gif 
←動画はこちら
正八面体は八面体対称である。そして正八面体を上のように８の破片に分割した図形も八面体対称である。この対称性は，破片が移動しても損なわれることはないから，爆発の全過程を通じて八面体対称は保たれている。
・正多面体による空間充填
８個の正三角錐は，３つの側面が互いに垂直。立方体の１つの頂点を，断面が正三角形になるように切り取った形をしている。これを４つ集めると，中に正四面体の空洞がある立方体ができる。正四面体の稜は立方体の各面の対角線と一致していて，正四面体は立方体に内接している。
ということは，稜長１の正八面体１つと，同じく稜長１の正四面体２つから，稜長√２の立方体が２つ作れるということだ。これは空間充填と関係がある。
たくさんの正八面体を，互いに稜が一致するように平行移動しながらつなげていく。そのとき，隣接正八面体の面同士は重ならず，間に隙間ができる。この隙間は，４つの正八面体の面で囲まれているので，正四面体である。
上右図で，正四面体の窪みができているのがわかるだろう。だから正八面体間の隙間を埋めると，正八面体と正四面体による空間充填になる。この空間充填において，正四面体は，周りの４つの正八面体から正三角錐を１つづつもらって立方体になれる。正八面体の周りには８つの正四面体があるから，この操作によって正三角錐は余らずに，立方体による空間充填が得られる。目を凝らして上右図を見れば，個々の正八面体の内部に隠れている稜線がその立方体の稜になっているのがわかる。
正多面体のみによる空間充填は，この二種類しか存在しない。その二種類が，このように相互に変換可能なのである。
・正八面体の爆縮
爆発とは逆に，破片が内側に飛んでいくとすると，どのような図形が得られるだろうか？破片同士は干渉せずに互いにすり抜けるとする。内側に爆発するのでこれを爆縮と呼ぼう。
初めのうちは，各角錐の頭頂点は，図形の内側に隠れていて表に現れてこない。角錐の底面付近が隣接する角錐底面と重なり合って縁取りのようになり，その縁取りがどんどん太くなっていく。
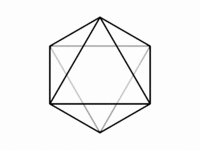
あるところで，一様多面体の星型切頂六面体が現れる（上右図）。一様多面体とは，正多角形のみでできていて，どの頂点も区別のつかない多面体である*1。正多面体や半正多面体は凸な一様多面体であり，星型正多面体は非凸な一様多面体である。
星型切頂六面体も非凸な一様多面体で，星型正八角形（正8/3角形）６枚と，正三角形８枚でできている。正八面体の破片は，正三角形を底面とし，底角45°の二等辺三角形*2を側面とする正三角錐なので，これ８個で，正三角形は８枚。二等辺三角形は24枚で，４枚づつ重なって星型正八角形を形づくる。
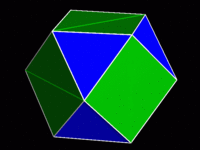
さらに移動が進むと，角錐の底面（正三角形）が内側，側面（直角二等辺三角形）が外側に来て，外形がまるっきり立方体になる。この状況がしばらく続いて，角錐相互の重なりが解消すると，角錐底面が立方八面体の正三角形の面の位置に来る。これは立方八面体にツノをつけた形になっている。立方八面体は，立方体を稜の中点まで切頂した形であって*3，ツノがまさに切られた頂点に該当する。
立方八面体の正三角形の面の位置は正八面体と共通だが，角度は60°ずれている。正八面体では，対向する平行な面がちょうど60°回転した関係にある（面心図参照）ので，正八面体の爆縮で立方八面体ができるのだ。
以上の過程を動画にしてみた→爆縮８.gif 
爆縮の場合も爆発の場合と同様に，全過程を通じて図形は八面体対称である。
・正八面体のひねり爆縮
この爆縮にひねりを加えてみよう。角錐を少しづつ回転させながら飛ばすのだ。ライフルの弾丸のように。このひねり爆縮の間，図形は八面体対称であるが，鏡映対称とは限らず，一般にキラルな図形になる。
回転角度をうまく調節して，角錐が自分の高さの２倍の距離移動したときに60°回っているようにしてみる。このとき角錐の底面は，もとの正八面体の面と一致しているので，これは正八面体にツノをつけた形になっている。爆縮が始まってからずっと失われていた鏡映対称性が，この時点で再び回復している。
動画はこちら→ひねり爆縮８.gif 
爆縮とひねり爆縮のいづれにおいても，その過程では，正三角錐８個からなる複合多面体*4が現れている。ひねり爆縮の場合，途中で角錐の底面が２個づつ一致して，双三角錐４個からなる複合多面体になる瞬間がある。右図に示したものが，その双三角錐４個の複合多面体である。もちろん正複合多面体*5ではない。
双三角錐ごとに色分けして表示したものも掲げておこう。
