2010-10-10

ペンローズ三角形

投影図

　小飼弾さんのブログをよく見るのだが，そこで紹介されていた，だまし絵の本がとても面白かった。杉原厚吉「だまし絵のトリック―不可能立体を可能にする (DOJIN選書34)」化学同人である。
　まだちゃんと読み終わっていないのだが，触発されて自分でもだまし絵を作ってみた。左は，最もよく言及されるだまし絵「ペンローズ三角形」である。三次元空間では不可能な図形のように見えることで超有名である。
　しかし，この図は3DCGソフトで作った三次元図形を，直投影風に二次元に描きあらわしたものである。本来の投影図は，多面体の稜のみをスクリーンに投影して得られた，線のみで描かれた図であるが，この図の場合は，立体からの平行光線がカメラのフィルムに像を結ぶようにして撮影した画像になっていて，立体を遠くから見た様子を表している。カメラとは別に，立体を照明するための光源も必要で，3DCGソフトは，三次元図形データとしての物体と，カメラ，照明光を三次元空間内に配置したときに，カメラに映る画像を作図してくれる。
　つまり，この図の示す立体は，あり得ない立体ではなく，ちゃんと実在する。不可能図形とされている「ペンローズ三角形」も，実は立体としてつくることが可能なのである。「だまし絵のトリック」では，不可能図形のだまし絵を分類し，立体として作ることが可能なものについて，たくさんの模型を掲げている。ボールが坂をひとりでに転がり上がるような不可能モーションについても触れられていて，それをつくるための模型の展開図も付いている。
　上のペンローズ三角形の種明かしをすると，下図のようになる。左は，直投影でなく透視投影風に描いたものである。つまり，近いものが大きく見え，遠いものが小さく見えるように，カメラを立体の近くにおいて，撮影したような図である。これを見れば，この立体は，実は三角形が閉じておらず，ただの三本の角棒を直角につないでいったものにすぎないことがわかる。手前の角棒の先端が斜めにカットされていて，直投影ではうまい具合にこの輪郭が奥の角棒の輪郭と一致していたにすぎない。透視投影では，図の左上の部分がつながっていないことが分かってしまう。

　上図右は，3DCGを描くときに立体を照らす照明を，無限遠からでなく有限の距離にある光源から当てたものである。よく見ないとわからないが，図の左上の部分に，冒頭に掲げた図には見られない線が入っているのがわかる。光源が近くにあるために，平行な面であっても，位置によって照明が当たる角度が異なるため，このように不完全なペンローズ三角形になってしまう。

　視点を遠くに置いた直投影に相当する図でも，見る角度を変えてしまうと，たちまち三角形の切れ目が露呈する。視点の角度が変わる様子を動画にしてみた。この動画は，ある角度から見るとペンローズ三角形に見える立体を，少しづつ角度を変えながら眺めた様子をあらわす。
ペンローズ三角形.gif
　結局，視点の距離，角度，照明の距離のすべてをうまい具合に選ばなければ，この立体はペンローズ三角形に見えないのである。
　考えてみれば，投影図に限らず，三次元図形を，二次元の図に描く場合，一枚の図ではどうしても元の立体の情報が抜け落ちてしまう。それでも通常は二次元的な図を一枚見るだけで，我々は立体の形をすぐに思い浮かべることができる。これはとても不思議なことだが，人間は経験に基づいて，足りない情報を補充して，立体的イメージを作っている。我々は二次元情報にすぎない図を見ても，ただちに立体感を感じ，直線だと直観する線を直線と解釈し，直角だと直感する角度を直角だと考える傾向がある。これは，直線や直角でできた物が身近にあふれているためだ。そしてその解釈は多くの場合に当たる。これを逆手にとったのがだまし絵である。経験による情報補充は厳密なものではないのだ。
　就学前後の子供は不可能図形をみても不思議に思わないらしい。十分な立体把握の経験がないためである。そのうち立体把握のための情報補充法を身につけると，以降，それは無意識で行われるようになり，だまし絵に対しても適用してしまうので，まんまとだまされる，というわけだ。

　最後に，3DCGソフトPOV-Ray用の，ペンローズ三角形のソースコードを以下に示しておく。ソフトはフリーでダウンロードできるので，それをインストールしてこのコードをコピペすると，冒頭のCGが得られるので，興味のある方は試してみてほしい。数値をいろいろいじると図も変わるので結構遊べると思う。

camera {
orthographic
location <50,50,50>
look_at <0, 0, 0>
angle 10
}

light_source {
<0,10,30>
color 1.5
parallel
point_at<0,0,0>
}

light_source {
<10,10,0>
color 0.5
parallel
point_at<0,0,0>
}

#declare Boxes =
merge{
box {<0,0,0>,<-1,-1,9>}
box {<-1,-1,9>,<8,0,10>}
box {<8,-1,10>,<9,8,9>}
pigment{rgb<1,0,0>}
}

#declare P_triangle =
difference{
object {Boxes}
box {<0,-1,-1>,<-2,2,2> rotate z*-45 translate <8,7,9> }
}

object { P_triangle no_shadow translate <-5,-3,-10>}
object { plane { z, -10 } pigment {rgb<1,1,1>} }

2010-10-08

正多面体の投影図

正多面体投影図

・投影法
　コンピュータのディスプレイも，紙の上も，縦横二次元の世界である。だから，そこに三次元図形を描くには，どうしても二次元の図形として描かなくてはならない。三次元図形を二次元図形に変換するのだが，このときにもっとも普通に行われる方法が投影法である。
　つまり，三次元空間内に，光源と，三次元図形と，スクリーンとしての平面を，この順で並ぶように配置し，スクリーン上に物体の影ができるようにして，映ったその影を求める二次元図形（投影図）とするのである。多面体をスクリーンに投影する様子を描いた図を掲げる。光源を白丸で示してある。
　このとき，多面体を不透明なものにしてしまうと，投影像は単なる中実の多角形になってしまい，多面体としての構造が皆目わからない*1。よって通常は，投影される多面体として，稜のみからなるフレームモデルを使用する。ただし，そのままでは稜同士の重なり具合が表現できず，立体感がなくなるため，光源から見て裏側に位置する稜の像を，点線や細線で弱々しく描いたり，又はまったく描かない，という隠線処理をする。

・直投影
　投影法には，光源の位置，形，スクリーンと光源との関係などによって，さまざまなものがあり，図学の教科書には網羅的な説明が載っている。中でも特に重要なのが，直投影と透視投影である。下に，立方体を直投影した図を示す。

　直投影とは，無限遠にある光源などによって平行光線をつくり，その光線と直交するようにスクリーンを配置して得られる投影である。直投影によると，スクリーンに平行な図形（多角形や線分）の投影像は，もとの図形と形もサイズも等しい合同な図形になる。スクリーンに平行でない線分は，直投影によって長さが変わる（短くなる）が，互いに平行な複数の線分は，直投影によってその長さの比を変えない。つまり，平行で等長な線分は，平行で等長な線分に投影される（このことは上図でも確認できる）。
　直投影において，線分とその像の長さの比は，それがスクリーンとなす角度θのみによって決まる。具体的にはこの比はcosθであり，スクリーンとの距離によらない。よって，直投影では遠近感が得られず，投影図はのっぺりした感じになる。直投影は，すべての光線がスクリーンと直交すればよいので，光源の位置を無限遠とするかわりに，光源をスクリーンに平行な無限平面としてもよい。

・透視投影
　これに対して，透視投影では，実際の見た目に近い，遠近感のある投影図が得られる。透視投影では，光源は点光源であり，スクリーンから有限の距離にある。初めに掲げた正二十面体の投影の様子は透視投影のものであった。立体上の点と，スクリーン上にできるその点の像を結ぶ直線は，一点（光源）で交わる。この関係は，人間が物体を見たり，カメラで物体を撮影する場合とまったく同様である。物体表面から出た光は，次第に収束して一点で交わった後再び拡がって，網膜上，又はフィルム上に像を結ぶ*2。

　上図左は立方体の透視投影の様子，右図は得られた投影図である。直投影とは異なり，平行な４本の稜の像が平行になっていないことがわかる。このように，透視投影では，互いに平行な線分が平行な線分に投影されない。互いに平行な線分の像は，延長するとある一点で交わり*3，これを消失点という。線分の長さの比も保たれない。そのため，透視投影図の描き方はなかなか煩雑である。

・正多面体の直投影
　直投影は，平行な線分の長さの比を保ち，スクリーンに平行な線分の長さを不変にするのであった。そのため，直投影図は比較的容易に作図することができる。逆に言うと，直投影では，多面体の寸法の情報を正確に表現することができ，これは幾何学的な考察にはとても都合がよい。以下では，特に正多面体の直投影について述べていく。
　直投影では，光線はスクリーンに垂直であるが，立体をどのような向きで配置するかによって，得られる投影像が異なってくる。正多面体においては，面心直投影，稜心直投影，点心直投影がよく使われる。これらは，正多面体の中心と，面の中心，稜の中点，頂点をそれぞれ結ぶ直線が，光線と平行になるような配置から得られる直投影である。面心直投影では，正多面体の面がスクリーンと平行，稜心直投影では，稜がスクリーンと平行になる。これら三種の直投影では，光線が正多面体の対称軸と平行になっているのがポイントであり，得られる投影図は，その対称軸の対称性と同等の対称性を備えている。

・正四面体
　正四面体の面心直投影は，構成面と合同な正三角形になる。隠線を描くなら，それは正三角形の中心と頂点を結ぶ線分になる。稜心直投影は，正方形に対角線を描き込んだものになる。一方の対角線は隠線である。点心直投影は，正三角形に，中心と頂点を結ぶ線分を加えたものである。面心，稜心，点心の各投影によって，正四面体の三回対称軸，二回対称軸，三回対称軸が中心の一点に投影される。それに応じて，面心図，稜心図，点心図は，それぞれ三回，二回，三回対称性をもっている。隠線を区別しなければ，稜心図は四回対称性を獲得する。

・立方体
　立方体の面心直投影は，正方形である。稜心直投影は，白銀長方形*4に，長辺の中点をつなぐ線分を描き込んだものになる。点心直投影は，正六角形に，中心と頂点を結ぶ線分を書き加えたもので，これらの線分を一つおきに選んだものは隠線である。面心図，稜心図，点心図は，それぞれ四回，二回，三回対称性をもつ。隠線を区別しなければ，点心図は六回対称性を獲得する。

・正八面体
　正八面体の面心直投影は，同心で逆さの正三角形を組み合わせたダビデの星に，六つの頂点をつないだ正六角形を加えたものになる。一方の正三角形の辺は隠線である。稜心直投影は，白銀菱形*5に，短い対角線を加えたものになり，点心直投影は，正方形に対角線を加えたものになる。面心図，稜心図，点心図は，それぞれ三回，二回，四回対称性をもつ。隠線を区別しなければ，面心図は六回対称性を獲得する。正八面体は立方体と双対であり，同一の回転対称性をもつから，一方の面心図と他方の点心図の対称性は等しく，両者の稜心図の対称性は等しい。

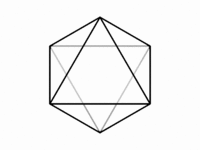
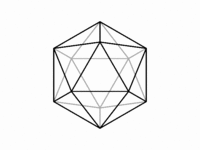
・正十二面体，正二十面体
　互いに双対な正十二面体と正二十面体の直投影は，次に掲げるようなものになる。正十二面体の面心図，稜心図，点心図は，それぞれ五回，二回，三回対称性をもつ。隠線を区別しなければ，面心図は十回対称性を獲得し，点心図は六回対称性を獲得する。正二十面体の直投影についての対称性は，面心図と点心図を入れ替えたものである。

*1:図では面を半透明にしている。

*2:実際には，眼やカメラには，水晶体やレンズがあるので，文字通りの直線ではないが，光にとっての直線は光線であり，物体上の点と，網膜上にできるその点の像を結ぶ光線は，一点で交わっている。レンズのないピンホールカメラであれば，物体上の点と，フィルム上にできるその点の像を結ぶ直線は，文句なしに一点で交わる。

*3:互いに平行な線分がスクリーンにも平行な場合は，線分の像も互いに平行であり，消失点はできない。この場合も線分の長さの比は保たれない。

*4:長辺の長さが短辺の長さの√２倍の長方形。√２は白銀比と呼ばれる。

*5:長い対角線の長さが短い対角線の長さの√２倍である菱形。

2010-10-06

別ブログを開設しました

　多面体の話題以外は，今後こちらのPolyhedronの非多面体日記につけようと思います。よろしくお願いします。

2010-09-23

ジタバグと正多面体

黄金比正多面体

・直交三長方形の凸包
　前回の記事で，中心で直交する３枚の長方形の頂点をつないで得られる多面体について触れた。凸多面体としては，一般には二十面体で，黄金長方形のときに正二十面体，長方形が正方形のときは立方八面体，長方形が線分に退化したときは正八面体が得られるのであった。

　前回のＣＧでは，３枚の長方形を変形させるときに，長方形の対角線の長さを保つように変形させていた。そのため，多面体の各面の大きさは，変形にともなって変化している。今回は，多面体を構成する８枚の正三角形の大きさが不変になるようにした（上図）。多面体の変形にともない，残りの12枚の二等辺三角形は，変形するものの，その等辺の長さは一定である。

・バッキーのジタバグ
　ここで，正三角形の面だけ残して二等辺三角形の面を消してみる。すると多面体は，８枚の正三角形が，頂点同士で相互につながった穴あきの形状になる。それぞれの穴を２枚の二等辺三角形で塞げば，もとの多面体が復元できる。

　これは次のような模型で実現できる。24本の等長な棒を，立方八面体の稜を構成するようにつなぎあわせる。棒のつなぎ目は，関節のように自由に回転できるようにしておく。すると，正三角形を囲む３本の棒は，相互に動くことができないが，正方形を囲む４本の棒は自由度があって動ける。これによって，模型を変形させることができ，それにともなって正方形の部分が変形する。辺の長さが一定なので，正方形は「菱形」に変形するが，この「菱形」は平面上になく，対角線で折れ曲がって三次元空間に飛び出している。
　正三角形の部分は変形しないので，面を貼ってもいい。ＣＧでは，稜のみにすると形状がつかみにくいので，そうせざるを得ないが，実際に模型をつくる場合は面がなくてもいい。この模型は，バックミンスター・フラーが「ジタバグ(Jitterbug)」と名付けたものである。フラーは二十世紀に活躍したアメリカの建築家で，フラードーム（測地線ドーム）やバッキーボール（フラーレン）にも名を残す有名人だ。
　立方八面体の状態から，穴の正方形を変形して，対向する頂点が稜の長さと等しい距離に近づいたとき，ジタバグは正二十面体の枠になっている。さらに変形して，対向する頂点間の距離がゼロになったとき，ジタバグは正八面体そのものになっている。この様子を動画にしてみた。
ジタバッグ.gif

・黄金二乗長方形と正十二面体
　この推移において，正二十面体と正八面体の間に，正十二面体と関係の深い状態がある。四角形の穴の対向頂点間距離と，稜長の比が黄金比になったとき，ジタバグは正十二面体に内接するのだ。ジタバグの12個の頂点が，外接正十二面体の頂点に一致する。正十二面体の頂点は全部で20個あるが，残りの８個は，ジタバグの正三角形の中心の上方にある。

　なお，穴の対向頂点は２組あって，各組で頂点間距離は異なるが，ジタバグが正二十面体に内接するとき，いづれの頂点間距離も，稜長との比が黄金比になっている。すなわち，
　近接頂点距離：稜長：遠隔頂点距離 $=1:\phi:\phi^2$ 　となっている。
　これは次のように言い換えられる。直交三長方形の凸包は，正三角形８枚，二等辺三角形12枚からなる二十面体であるが，二等辺三角形が黄金三角形になるとき，二十面体は正十二面体に内接する。このとき，12枚の黄金三角形は正十二面体の各面に現れる大きな黄金三角形と一致している。もとになる長方形は，短辺と長辺の長さの比が $\phi^2$ である。いわば，黄金二乗長方形だ。
　結局，中心で直交する３枚の黄金二乗長方形の凸包は，正三角形８枚，黄金三角形12枚からなる二十面体であり，正十二面体に内接する。この二十面体と正十二面体は，12個の頂点が一致し，正十二面体の残りの８頂点は，立方体の頂点と一致する。この立方体は，もとの黄金二乗長方形と同心で，立方体の稜長は，黄金二乗長方形の長短どちらの辺の長さとも黄金比になっている。つまり，
　長方形短辺の長さ：立方体の稜長：長方形長辺の長さ $=1:\phi:\phi^2$ 　となっている。

・ジタバグと正多面体
　ジタバグは，８枚の正三角形からなるが，正八面体の状態からさらに畳んでいくと，面が重なって正四面体を作ることもできる。そして，立方八面体の形態において，ジタバグは立方体に内接する。このとき，ジタバグの12頂点は立方体の稜の中点に一致し，立方体の面がジタバグの穴をぴったり塞ぐような配置になる。
　結局，ジタバグは，最も大きな立方八面体の状態から，どんどん小さく畳んでいくことによって，５つの正多面体すべてを経由する。立方体→正二十面体→正十二面体→正八面体→正四面体の順である。

　正四面体を除く４つの正多面体は，変形する直交三長方形の凸包から出てくる。凸包は，長方形が正方形のとき立方体に内接し，黄金長方形のとき正二十面体と一致し，黄金二乗長方形のとき正十二面体に内接し，長方形が線分に退化するとき正八面体と一致する。

凸包	立方体に内接*1	正二十面体	正十二面体に内接	正八面体
直交三長方形	正方形	黄金長方形	黄金二乗長方形	線分
二等辺三角形	直角二等辺三角形 *2	正三角形	黄金三角形	線分

*1:立方八面体

*2:斜辺を共有する２枚が面一となって正方形になる

2010-09-20

黄金長方形と正二十面体

正多面体黄金比

・直交三長方形の凸包

　三次元空間で，合同な長方形を三枚，中心を一致させて直交させることができる。このとき，長方形の長軸も互いに直交するようにする。
　この図形自体は各面の縁が孤立しているので多面体ではない。しかし，これを枠としてまわりに面を貼れば立派な多面体になる。３枚の長方形の短辺だけ残してこれを６本の稜とし，その両端の計12個の頂点を，近くの頂点とつないで新しい稜とし，最後に面を貼ると，二十面体になる。

　この多面体はもとの直交三長方形の凸包*1である。ある図形の凸包とは，おおざっぱに言えば，その図形をすっぽり包む最小の凸多面体である*2。
　もう少し正確には，凸包とは次のような形である。もとの図形を大きな立体にすっぽり埋め込んで，もとの図形を決して削らないように，とても注意深く平面グラインダーでやすりがけをする*3。そうして削っていって，もう削るところが一切なくなったときに得られる立体がもとの図形の凸包である*4。こうしてできる凸包は，多面体とは限らず，曲面をもっている場合もある。ある方向に無限に広がる（有界でない）図形になる場合もあるが，必ず凸図形になる。

　直交三長方形の凸包は，一般には二十枚の三角形からなる二十面体である。二十枚の三角形は２種類に分けられる。３枚の長方形の頂点をつないだ青で示した面と，１枚の長方形の短辺と他の１枚の長方形の頂点をつないだ緑で示した面である。前者は８枚あって，合同な正三角形であり，立方体の頂点の方向にある。直交する三枚の長方形をｘｙ，ｙｚ，ｚｘ平面に置けば，８つの象限それぞれにある。後者は残りの12枚で，すべて合同な二等辺三角形であり，これは立方体の稜の方向にある。この12枚は，長方形の短辺を共有する２枚が１組となって，６組ある。各組は立方体の面の方向にある。

・退化する二十面体

　凸包は一般的には二十面体だが，特別な場合にはそうでなくなる。まず，三枚の長方形が正方形の場合は，凸包は立方八面体になる。12枚の二等辺三角形が直角二等辺三角形になり，各組において斜辺を共有する２枚が面一となって正方形に退化するためである。つまり，中心を共有し，面も軸も互いに直交する３枚の正方形の凸包は，立方八面体である。

　短辺が短くなった極限，つまり長方形が線分になる極限を考えると，二十面体は八面体に退化する。なぜならこの場合，12枚の二等辺三角形は，底辺が１点に退化するために線分に退化してしまうからである。残るのは８枚の正三角形だけである。すなわち，中点を共有する等長な直交三線分の凸包は，正八面体である。

・正二十面体と黄金長方形

　二等辺三角形が正三角形になった場合，二十面体は正二十面体になる。このときの長方形はいかなる長方形であろうか。
　長方形の短辺の長さを $2$ とし，長辺の長さを $2a$ とする。 $a\ge1$ である。すると，直交させた三枚の長方形の頂点座標は，それぞれ， $(\pm1,\pm{a},0)$ ， $(0,\pm1,\pm{a})$ ， $(\pm{a},0,\pm1)$ である。このうち，第一象限にある頂点は $(1,a,0)$ ， $(0,1,a)$ ， $(a,0,1)$ であるが，この３点のうちどの２点間距離も， $\sqrt{2(1-a+a^2)}$ である*5。
　この距離が，長方形の短辺の長さと等しければ，残りの二等辺三角形も正三角形となる。その条件は， $1-a+a^2=2$ ，すなわち， $a^2=a+1$ 。この等式は，黄金比の定義にほかならない。すなわち，中心を共有し，面も軸も互いに直交する黄金長方形の凸包は，正二十面体である。

・非凸多面体への拡張

　以上，凸包としての凸多面体を考えてきたが，面の貼り方を変えずに，長方形の短辺と長辺を入れ替えると，非凸な多面体ができる。自己交差のない凹二十面体である。つまり，同一象限にある３枚の長方形の頂点をつないで正三角形とし，１枚の長方形の長辺と他の１枚の長方形の頂点をつないで二等辺三角形をつくる。長方形の長辺を共有する二枚の二等辺三角形の部分は切り込みを入れたようにへこんでいる。黄金長方形からこれをつくると，正二十面体の面を12枚を外して，その穴を，くさび状に組み合わせた計12枚の二等辺三角形で埋めた凹二十面体ができる（上図）。

　頂点のつなぎ方をかえずに長方形を裏返してやると自己交叉多面体が得られる。例えば長方形をすべて長軸に関して裏返し，短辺両端の頂点をすべて入れ替えてやるのだ。すると８つの方向を向く正三角形は正八面体のときよりも大きくなって互いに交差する。その中でも最も対称なのは大二十面体だ。星型正多面体の一つである。
　三つの黄金長方形を中心で直交させて，長辺を残して他の頂点とつなぐと凹二十面体になるが，この状態から黄金長方形を長軸まわりに裏返すと，大二十面体が得られるのである（上図）。20枚の面はすべて正三角形になっている。

・動画
　静止画だけではイメージがつかみにくいかもしれないので，この一連の多面体間の推移をアニメにしたものを紹介する。
・多面体のみのもの　循環.gif
・もとになる長方形のみのもの　長方形.gif
・長方形と多面体をあわせたもの　長方形も.gif
　大二十面体が回転するアニメもつくってみた。　大二十面体.gif

*1:ある図形の凸包とは，その図形上の点をすべて含む最小の凸集合である。凸集合とは，空間内に配置された点を要素とする集合であり，集合の中からどの２点を取ってきても，それを結ぶ線分上の点が必ずその集合の要素に含まれるような集合である。

*2:もとの図形は全体がつながっていなくてもよく，ばらばらな点の集合でも構わない。多角形や多面体といった普通の連結な図形は無限個の点の集合である。はじめの図形によっては，凸包は表面が曲面になったり，無限に広がって凸多面体にならないこともあるが，有限個の点の集合の凸包は必ず凸多面体になる。

*3:あるいはもとの図形は無限に硬くて削れないとしてもよい。グラインダーも無限に硬くて決して変形しないとする必要がある。

*4:この直交三長方形の凸包は，計12個の頂点の凸包と一致する。一般に，凸多面体は，そのすべての頂点を要素とする集合の凸包である。凸包が凸多面体となる点の集合にはさまざまなものが存在するが，そのうち最も要素数の少ないものは，その凸多面体の頂点の集合であり，それに限られる。

*5:これは二十面体の八面が正三角形であることの確認になっている。

2010-09-16

黄金比と正五角形

黄金比

　正五角形の辺長と対角線長の比 $\phi$ は黄金比である。いままで，対角線の長さの比が黄金比であるような黄金菱形多面体について述べてきたが，黄金比について詳しくは触れなかった。黄金比 $\phi$ は約1.61803という値をもつ無理数である。非常に興味深い性質を備えている重要な数であるので，補足しておく。

・黄金比の値
　正五角形の辺と対角線の比 $\phi$ は次のようにして求められる。

　辺長１の正五角形ABCDEに，対角線AC，AD，BEを引く。ADとBC，BEとCDは，それぞれ平行である。AC，ADとBEの交点をP，Qとして，△ACDと△CPBを見ると，錯角相等よりこれらの三角形が相似であることがわかる。しかもこれらは二等辺三角形であり，それぞれの等辺の長さが，AC=AD= $\phi$ ，CP=CB=1であるから，相似比は $\phi:1$ である。
　よって， $PB=\frac{CD}{\phi}=\frac{1}{\phi}$ 。対称性から，PA=PB。一方，PA=AC-CP= $\phi-1$ でもある。
　したがって， $\frac{1}{\phi}={\phi}-1$ であり，これを変形すると， $\phi^2=\phi+1$ を得る。
　そもそも黄金分割とは，線分をある点で異なる長さに２分割して，短い断片と長い断片の長さの比が，長い断片ともとの線分の長さの比に等しくなるように分割することで，その比を黄金比というのである。外中比ということもある。
　 $\phi^2=\phi+1$ という等式は，線分＝長片＋短片に対応し，まさにそのことを示している。正五角形の対角線は，互いに他を黄金分割することが分かった。
　すなわち， $\phi$ は，二次方程式 $x^2-x-1=0$ の正の解である。これを解いて， $\phi=\frac{1+\sqrt{5}}{2}$ と求まる。

・黄金比の整数乗
　黄金比の混じった計算をするときに，式変形に非常に有用な性質がある。黄金比及びその逆数の有理多項式は，必ず黄金比の有理一次式で書ける，という性質である。特に，黄金比の整数乗は，整数×黄金比＋整数の形に書ける。
　 $\phi^2=\phi+1$ 　から次々に， $\phi^3=2\phi+1$ ， $\phi^4=3\phi+2$ ， $\phi^5=5\phi+3$ ， $\phi^6=8\phi+5$ 　を導くことができ，
　 $\frac{1}{\phi}=\phi-1$ 　から次々に， $\frac{1}{\phi^2}=2-\phi$ ， $\frac{1}{\phi^3}=2\phi-3$ ， $\frac{1}{\phi^4}=5-3\phi$ ， $\frac{1}{\phi^5}=5\phi-8$ ， $\frac{1}{\phi^6}=13-8\phi$ 　を導くことができる。
　係数と定数項に出てくるのは，フィボナッチ数である。

・三角比

　正五角形に対角線を引いたときに現れる鋭角二等辺三角形は，すべて相似である。正五角形の頂点に集まる３つの角は，いづれもその頂角であるからすべて等しい。すなわち，正五角形の対角線は，内角を三等分する。正五角形の内角は108°であるから，鋭角二等辺三角形の頂角は36°であり，底角は72°である。

　これから36° $=\frac{\pi}{5}$ についての三角比が求められる。△ABCにおいて，BからACに下ろした垂線の足をHとすると，HはACを二等分するから，
$\cos\frac{\pi}{5}=\frac{AH}{AB}=\frac{\phi}{2}$
$\sin\frac{\pi}{5}=\sqrt{1-\cos^2\frac{\pi}{5}}=\frac{\sqrt{4-\phi^2}}{2}=\frac{\sqrt{3-\phi}}{2}$
$\tan\frac{\pi}{5}=\frac{\sin\frac{\pi}{5}}{\cos\frac{\pi}{5}}=\frac{\sqrt{3-\phi}}{\phi}$

・正五角形と黄金比
　正五角形に対角線を引くと，黄金比が至る所に現れる。黄金比しか現れないと言ってもいいくらいだ。

　まず，一本の対角線には，他の対角線で分断されて４種類の長さが現れている。小さい方からPQ，PB=QE，BQ=EP，BEであるが，これらの長さの比は， $1:\phi:\phi^2:\phi^3$ になっている。すなわち，この４種の長さのうち近接する２種の長さの比は，どれも黄金比になっている。図から， $\phi^2=\phi+1$ ， $\phi^3=2\phi+1$ であることが一目瞭然である。

　五芒星のトゲの部分に小さな鋭角二等辺三角形が５個あり，これより大きい相似な二等辺三角形と，さらに大きい相似な二等辺三角形があるが，これらの相似比は， $1:\phi:\phi^2$ である。すなわち，これら３種の鋭角二等辺三角形は，小：中も，中：大も，黄金比になっている。

　五芒星の外側に小さな鈍角二等辺三角形が５個あり，これより大きい相似な二等辺三角形が一種類あるが，これらの相似比は黄金比である。
　もちろん，相似比が黄金比であるということは，面積比は黄金比の二乗であるということだ。

　小さい鋭角二等辺三角形と小さい鈍角二等辺三角形の面積比は，黄金比である。左図を見ると分かるように，高さが同じで底辺の長さの比が黄金比だからだ。
　よって，鋭角鈍角交互に小さい順に並べた５種類の三角形の面積の比は， $1:\phi:\phi^2:\phi^3:\phi^4$ となっている。下図を参照されたい。

　正五角形の辺を上底とし対角線を下底とする等脚台形の面積は，大きい鋭角二等辺三角形と大きい鈍角二等辺三角形の和なので，大きい鋭角二等辺三角形の面積の $1+\frac{1}{\phi}=\phi$ 倍であり，大きい鈍角二等辺三角形の面積の $1+\phi=\phi^2$ 倍である。

　正五角形は，この等脚台形と鈍角二等辺三角形でできているから，一本の対角線は，正五角形の面積を $1:\phi^2$ に分割する。
　正五角形の面積は，小鋭角二等辺三角形の $2\phi^3+\phi^4$ 倍である。大鈍角二等辺三角形２個と大鋭角二等辺三角形１個の面積を足すと，正五角形の面積になるからだ。

　また，一本の対角線は，正五角形の高さを黄金分割する。分割して得られる等脚台形の高さは，その内部の大鋭角二等辺三角形の等辺を「底辺」と考えたときの高さに等しいところ，大鈍角二等辺三角形と大鋭角二等辺三角形は「底辺」を共有し，面積比が黄金比だからである。

　正五角形の芯には小さい正五角形が存在する。もとの大正五角形は，この小正五角形を $\phi^2$ 倍に拡大したものであり，面積は $\phi^4$ 倍ある。よって，小正五角形の面積は，小鋭角二等辺三角形の $\frac{2}{\phi}+1=2\phi-1=\phi+\frac{1}{\phi}=\sqrt{5}$ 倍である。
　ということは，大きい正五角形の面積も，大きい鋭角二等辺三角形の√５倍である。

・黄金長方形
　辺の長さの比が黄金比の長方形を，黄金長方形という。

　黄金長方形から，最大の正方形を図のように切り出すと，残った長方形もまた黄金長方形になる。なぜなら，大長方形の辺長を１， $\phi$ とすると，小長方形の辺長は $\phi-1$ ，１であるが，先に見たように $\phi-1=\frac{1}{\phi}$ なので，小長方形の辺長比もまた黄金比になるからである。この２つの黄金長方形の相似比もまた黄金比である。
　この手続きは，いくらでも続けて行なうことができる。次に切り出す正方形と前に切り出した正方形の相似比も黄金比である。
　ちなみに，辺の長さの比が白銀比（√２）の長方形を，白銀長方形という。白銀長方形を２つに折りたたむとそれも白銀長方形になる。すなわち，白銀長方形は，２つの小さい白銀長方形に二等分できる。大小の白銀長方形の相似比もまた白銀比である。この手続きも，いくらでも続けて行なえる。Ａ４とかＢ５とかの用紙は，だいたいこの白銀長方形になっている。

・黄金三角形

　底辺と等辺の長さの比が黄金比の鋭角二等辺三角形を，黄金三角形という。黄金三角形は，正五角形に対角線を引いたときに現れる，頂角が36°，底角が72°の二等辺三角形である。

　黄金三角形の底角を二等分すると，小さい黄金三角形が現れ，残りの部分も二等辺三角形になる。大小の黄金三角形の相似比はもちろん黄金比である。
　頂角が底角のちょうど半分であるところがポイントで，そのような二等辺三角形は黄金三角形に限られる。この入れ子の様子は，正五角形に対角線を引いたときにちょうど３つ分が現れている（右図）。黄金長方形の分割と同様，黄金三角形の分割も際限なく行なえる。

2010-09-06

正四角反柱の輪

整凸多面体

　hhaseさんの「あそびをせんとや」に，正四角反柱の輪についての記事が書かれている。等稜正四角反柱の模型を，対向する正三角形の面でどんどんつないでいくと，13個で環状になるそうだ。13個とは随分半端な数で，おそらく両端に隙間が残るか重なると思われる。自明ではないのでこれを計算してみた。

　正四角反柱の底面側面間の二面角を $\theta$ とすると，正四角反柱を環状につなぐときの１つ分の角度は，対向する側面がなす角に等しいから， $2(\theta-\frac\pi{2})$ となる。
　よって13個分だと， $26(\theta-\frac\pi{2})$ 。これが， $2\pi$ ＝360°に一致するかどうか調べればよい。

　正四角反柱の上下底面は，真上から見ると中心が一致して角度が45°ずれているから，
下面の頂点の座標を $(\pm1,\pm1,0)$ とし，高さを $h$ とすると，上面の頂点の座標は $(\pm\sqrt{2},0,h),(0,\pm\sqrt{2},h)$ と書ける。
代表する点として， $A(1,1,0),B(\sqrt{2},0,h),C(1,-1,0)$ の三点をとり，これらを頂点とする三角形 $ABC$ が，正三角形であることから， $h$ を算出する。
この三角形の辺長は，2であるから， $AB$ の長さの自乗は，
$(\sqrt{2}-1)^2+h^2+1^2=2^2$
これを解くと， $h=\sqrt{2\sqrt{2}}$ が得られる。

三角形 $ABC$ において， $B$ から $AC$ に下ろした垂線の足は $AC$ の中点 $H(1,0,0)$ であり，求める二面角 $\theta$ は， $BH$ と $x$ 軸のなす角である。
よって， $\tan\theta=\frac h{1-\sqrt{2}}$
$\theta=\tan^{-1}(\frac{\sqrt{2\sqrt{2}}}{1-\sqrt{2}})$
よって， $\theta$ ≒103.8362°となり， $26(\theta-\frac\pi{2})$ ≒359.7402°

かなり近いが，360°に一致しない。誤差は僅か0.2598°で，なんと千分の一以下である。驚くほど誤差が小さい。

輪がぴったり一致しないことは，次のように考えても分かる。
もし正四角反柱13個をぴったり環状につなげるなら，この環の内周も外周も正十三角形になっているはず。これらの正十三角形の辺長の比は， $1:\sqrt{2}$ なので，各々の辺長を $2,2\sqrt2$ と置くと，
内側の正十三角形の内接円半径は， $\frac1{\tan\frac{2\pi}{26}}$ 。
外側の正十三角形の内接円半径は， $\frac{\sqrt2}{\tan\frac{2\pi}{26}}$ 。
これらの差は， $\frac{\sqrt2-1}{\tan\frac{2\pi}{26}}$ ≒1.68053。
$h=\sqrt{2\sqrt{2}}$ ≒1.68179であるから，僅かに異なる。つまり完全な環にはならない。

　上の議論は，次のようにして正２ｎ角反柱に一般化できる。
下面の頂点の座標を $(\cos{\frac{(k+\frac1{2})\pi}{n},\sin{\frac{(k+\frac1{2})\pi}{n},0)$ とし，上面の頂点の座標を $(\cos{\frac{k\pi}{n},\sin{\frac{k\pi}{n},h)$ とすると，
同様の計算により， $h=\sqrt{2(\cos{\frac\pi{2n}}-\cos{\frac\pi{n}})}$
$\tan\theta=\frac{h}{\cos{\frac\pi{2n}}-1}=\frac{\sqrt{2(\cos{\frac\pi{2n}}-\cos{\frac\pi{n}})}}{\cos{\frac\pi{2n}}-1}$
ただし，正二角反柱たる正四面体*1は，底面が線分（稜）に退化しているので，底面側面間の二面角を考えることはできない。よって，ｎ≧２である。
ちなみにｎ＝１の場合は， $\theta$ は二面角ではなく，対向する側面がなす角 $2\theta-\pi$ そのものが正四面体の二面角になる。 $\theta$ を計算すると，
$\theta=\tan^{-1}{\frac{\sqrt{2(\cos{\frac\pi{2n}}-\cos{\frac\pi{n}})}}{\cos{\frac\pi{2n}}-1}}$
この値は約125.26439°なので，正四面体の二面角は約70.5288°と求まる。よって，正四面体を１つの稜周りに環状に並べていくと，５個並べたところで7.3561°あまりの隙間が残る。

$n$ にいろいろな数を入れて試してみたが，ぴったり環状になる反角柱は見つからない。存在しないんじゃないかと思うが，証明はどうやるんだろう？近いものならある。
正24角反柱なら，83個でほぼ環状になる。角度はやや過剰で，誤差は $\frac{2}{1000000}$ くらい。
正54角反柱では，187個で僅かに角度が過剰になる。誤差は $\frac{4}{10000000}$ くらい。
これらは誤差こそ小さいものの，つなぐ数が無闇に多いし， $n$ を多少増減しても反角柱があまりかわりばえしないので，それほど面白い結果ではない。やはり正四角反柱13個というのが興味深く，味わい深い。

もちろん以上はすべて等稜反角柱の話であり，側面を正三角形に限らなければ，ぴったり環状になるように調節することは可能だ。つまり，側面が二等辺三角形でよければ，高さをうまく調節して，任意の正２ｎ角反柱（ｎ≧１）に対して，３以上の任意の個数でぴったり環状になるようにつなぐことができる。

*1:上底面が正ｎ角形，下底面が正２ｎ角形，側面に正方形と正三角形が交互に並ぶ，「ｎ角台塔」という多面体があるが，二角台塔は正三角柱である。これはアルキメデスの角柱なので，ジョンソンの立体には入らないが，三角台塔，四角台塔，五角台塔や，二角台塔を下底面で貼り合わせた双二角反台塔（異相双三角柱）はジョンソンの立体である。ジョンソンの立体について詳しくはこちら。なお，正三角反柱は，正八面体である。