2011-01-17

正十二面体の十二等分

・正十二面体の体積
　稜の長さが１の正十二面体の体積 $V$ を求めることを考える。どうすればいいか。

　一番簡単なのは，正十二面体を12個の合同な正五角錐に分解して，その正五角錐の体積を12倍することだろう。正十二面体の中心と各稜を結ぶと，合同な正五角錐に12等分することができる。*1正五角錐の底面は，辺長１の正五角形で，高さは正十二面体の内接円の半径に等しい。

　正五角形の面積は，次のようにして求まる。正五角形を二本の対角線で分割すると，鈍角黄金三角形２つと鋭角黄金三角形１つが得られる。鋭角黄金三角形の底辺長は１，等辺長は $\phi$ である。*2
　よってピタゴラスの定理より，鋭角黄金三角形の高さは， $\sqrt{\phi^2-(\frac{1}{2})^2}=\frac{\sqrt{4\phi+3}}{2}$
　なので，鋭角二等辺三角形の面積は， $\frac{\sqrt{4\phi+3}}{4}$ 。
　鈍角黄金三角形の面積は，この $\phi$ 分の１，すなわち $\phi-1$ 倍なので，正五角形の面積 $S$ は，鋭角二等辺三角形の面積の $1+2(\phi-1)=2\phi-1(=\phi+\frac{1}{\phi})=\sqrt{5}$ 倍になる（過去エントリ参照）。
　よって，正五角形の面積は， $S=\frac{\sqrt{5(4\phi+3)}}{4}\simeq1.720$

　正十二面体の内接球の半径 $r_i$ は，以前稜心図から求めてあった。
　 $r_i=\frac{\phi^3}{2\sqrt{\phi+2}}\simeq1.114$
　結局，正十二面体の体積は， $V=\frac{12}{3}Sr_i=\frac{\sqrt{5(4\phi+3)}\phi^3}{2\sqrt{\phi+2}}\simeq7.663$ 。すなわち，稜長１センチの正十二面体の体積は，約7.663立方センチ。稜長の等しい立方体の体積の7.663倍である。かなり大きいが，実際稜長を揃えたとき，五種の正多面体の中で正十二面体の体積がダントツに大きくなる*3。

・正十二面体の爆発と爆縮
　正十二面体が爆発して12個の角錐破片が外へ飛んでいく様子を動画にしてみた→爆発.gif 。
　この逆に，もし破片が内側に飛んでいくとすると，どうなるだろうか。破片同士は干渉せずに互いにすり抜けるとする。おなじみの多面体にとてもよく似た形が現れるのだが…。分かった方はコメント下さい。質問もお気軽にどうぞ。（1/18修正）

*1:正多面体の中心と各稜を結ぶと，合同な正多角錐に分割することができる。

*2:鈍角の等辺と，鋭角の底辺の長さは１で，鈍角の底辺と，鋭角の等辺の長さは $\phi$ である。

*3:ちなみに，稜長１の正多面体の体積は，正四面体が約0.118，立方体が１，正八面体が約0.471，正十二面体が約7.663，正二十面体が約2.182。他の四種の体積をすべて合わせても，正十二面体の半分に満たない。

2010-12-06

正多面体と正多角形の多義性

正多面体

・言葉と意味の対応関係
　日本語に限った話ではないが，言葉の意味というのは，はっきりと決まったものではない。同じ言葉でも，文脈とか文化に応じて，その意味はさまざまに変わりうる。発言者の意図した意味が，聴取者にしっかり伝わらないことがある。著書の記述の一部だけを引用して批評することや，言葉の一部だけを切り取って報道することもしばしば行なわれ，理不尽な批判になっていることも少なくない。言葉がこんなに曖昧なものであることは，一見デメリットに思える。もっと間違いのない，論理的な言葉というのはないのだろうか。
　しかし，言葉と意味が一対一対応しないのは，言葉の本質である。しかも，それは欠点ではなく利点である。社会の仕組みや人々の意識は時の経過とともに変化していくので，既存の言葉の意味が金輪際変わらないとすると，社会の変化に対応できない。というか，話は逆で，言葉の意味にある程度の柔軟性がなければ，世の中が変化しようがない。暗黒の中世においてさえ，言葉は常に変化してきた。社会の変化が激しくなり，情報交換が活発になるほど，言葉の変化も顕著になる。

・用語と意味の対応関係
　ただ，学問的な議論をしようとするときは，用いる言葉の意味が曖昧では，厳密な議論ができない。言葉と意味との一対一対応は，科学においては切実で，数学においてはほとんど不可欠の要請である。人文系の議論においても，決して疎かにはできない。疎かにすると学問ではなくなってしまう。だから学術用語では，なるべく言葉と意味を一対一対応させる。しかしそれでも，完全に特定の意味でしか使われない学術用語というのは，ごくごく少数の基本語彙だけである。誤解の恐れのある用語を用いる場合は，文章中で前もってその用語をどんな意味で使うのか，定義しておく必要がある。

・多面体の多義性
　さて，我らが「多面体」という言葉も，多義的であることを免れていない。それほど厳密に考えなくても，四つの異なる意味が挙げられる。最も狭義に「多面体」と言うと，凸多面体を指すだろう。一部がへっこんでるのや孔の空いたのは，一般的には多面体と考えにくい。もう少し広げて狭義には，多面体とは自己交叉のないものを指すだろう。面と面が交叉しているようなものは，面に余計な切り込みを入れなければ模型にできず，忠実な模型を作ることができないからだ。広義には，多面体とは自己交叉のあるものも含まれる。一般に「多面体」と言う場合，この広義の意味であることが多い。
　最広義には，複合多面体まで含まれる。面が連結でないから，複合多面体は多面体ではない，と以前書いたが，そのときの「多面体」は広義の多面体であった。組み立て途中の展開図のように，複数の多角形でできていても，多角形の辺が孤立しているようなのは最広義の多面体にも入らない。
　この意味では，最狭義及び狭義の正多面体がプラトンの立体であり*1，広義の正多面体になると星型正多面体が加わり，最広義の正多面体には正複合多面体も含まれる，ということになる。さらに異なる意味での「正多面体」も考えることが可能である。正スポンジと呼ばれる３種があったり，三次元以外にも正多面体に相当する図形がある。しかし，前者は有限の領域に収まらないので「多面体」という感覚からかなり外れてしまうし，後者は正多角形や正多胞体という別の用語が用意されているので，除外することとしよう。

	最狭義	狭義	広義	最広義
多面体	凸多面体のみ	非自己交叉多面体も含む	自己交叉多面体も含む	複合多面体も含む
正多面体	プラトンの立体５種	プラトンの立体５種	星型正多面体も含む９種	正複合多面体も含む14種

　さて，本稿中，以降で「多面体」とは，特に断らない限り複合多面体を含む最広義の意味で用いる。正多面体は，14種（１種はキラル）あり，すべての面，すべての稜，すべての頂点の区別がつかない多面体である。

↑正四面体，立方体，正八面体，正十二面体，正二十面体

↑小星形十二面体，大星形十二面体，大十二面体，大二十面体

↑正四面体×２，正四面体×５，正四面体×10，立方体×５，正八面体×５

・正多角形の多義性
　正多面体はもちろん三次元図形であるが，二次元図形に正多面体に相当する図形はいくつあるだろうか。そのような図形を正多角形と呼ぼう。すべての面，すべての辺の区別がつかない多角形を，自己交叉するものも含めて正多角形と呼ぶのである。
　まず，狭義の正多面体に相当するのは，凸な正多角形であり，無限に存在する。そして，広義の正多面体に相当するのは，狭義の星型正多角形まで含めた正多角形である。このような星型正多角形に該当するのは，mとn(m>2n)が互いに素な場合の正m/n角形である。等しい長さのm本の辺がすべて一つながりになって，等しい角度で頂点を挟んでいる。星型正五角形（正5/2角形），すなわち五芒星（ペンタグラム）が代表例であるが，これも無限に存在する。
　最広義の正多面体に相当するのは，広義の星型正多角形まで含めた正多角形である。このような星型正多角形には，m/nが通分できる場合の正m/n角形が該当する。等しい長さのm本の辺が，等しい角度で頂点を挟んでいるが，一つながりになってはいない。辺が連結でないから，いわば正複合多角形である。凸な正多角形が複合したものと，狭義の星型正多角形が複合したものの２系列があり，いづれも無限に存在する。前者の代表は星型正六角形（正6/2角形），すなわちダビデの星であり，正三角形が二つ複合している。正三角形は正四面体の二次元相当物であるから，それを二つ組み合わせたダビデの星は，ケプラーの星の二次元相当物といえる。後者の代表は，正10/4角形であり，星型正五角形が二つ複合している。m/nを通分したときの値が整数になるのが凸正多角形の複合体，整数にならないのが（狭義の）星型正多角形の複合体である。

	狭義	広義	最広義
正多面体	プラトンの立体５種	星型正多面体も含む９種	正複合多面体も含む14種
正多角形	凸正多角形	狭義の星型正多角形も含む	広義の星型正多角形も含む（＝正複合多角形も含む）

　正多角形は，すべての面，すべての稜の区別がつかない多角形であり，凸正多角形，狭義の星型正多角形，正複合多角形の各系列が，いずれも無限に存在する。正複合多角形には，凸正多角形の複合体が無限にあり，星型正多角形の複合体も無限にある。これに対し，三次元の正複合多面体に，星型正多面体の複合体が存在しないのは興味深い。星型正多面体はすべて二十面体対称なので，正十二面体や正二十面体と同様，正複合多面体を作れないのだ。

↑正五角形，正六角形，正七角形，正十角形，正十二角形

↑正5/2角形（星型正五角形），正7/2角形，正7/3角形，正10/3角形，正12/5角形

↑正6/2角形（星型正六角形），正10/2角形，正12/3角形，正12/4角形，正10/4角形

・星型正多角形の芯と凸包
　正多面体のうち，凸でないものは，凸包と芯をもっていた。凸包も芯も凸多面体であり，凸包の頂点のつなぎ具合を変えることや，芯を星型化することで，もとの非凸正多面体が得られる。そして，双対な正多面体同士で，一方の凸包は他方の芯と双対であった。自己双対な正多面体では，自分の凸包と自分の芯が双対である。この関係は，正多角形も共有する*2。
　正多角形も，凸でないものは，凸包と芯をもつ。凸包も芯も凸な正多角形であり，凸包の頂点のつなぎ具合を変えることや，芯を星型化することで，もとの非凸正多角形が得られる。正m/n角形について，凸包も芯も凸な正m角形である。つまり，自分の凸包と自分の芯が同じ正多角形になる。正多角形は，凸なものも非凸なものも，すべて自己双対なので*3，双対な非凸正多角形同士で凸包と芯が互いに双対という関係は満たされている。
　二次元では何の変哲もない凸包・芯と双対の関係が，三次元ではより豊かで興味深い関係になっている。しかもそれを特別な場合として含む形で，である。なんだか，アインシュタインの相対性理論が，ニュートン力学を含む形で適用範囲を拡大したのと似ている。思えばニュートン力学も，それまで天界と月下界で異なるとされていた法則を，統一的に説明するという画期的な拡張だった。

*1:正則という条件がついたために最狭義と狭義の区別がなくなっている。煩雑なので適宜まとめて「狭義」とする。

*2:多面体について双対とは，面と頂点を入れ替えたものであったが，多角形について双対とは，稜と頂点を入れ替えたものである。

*3:正多角形に対し，稜の中点を，隣接する稜の中点と結ぶ操作を繰り返すと，双対な正多角形が得られるが，この操作によってもとと同じ正多角形が得られる。

2010-11-18

正複合多面体の凸包と芯

正多面体

・正則な多面体と複合多面体
　すべての面，すべての稜，すべての頂点がそれぞれ区別できない凸多面体は，５種の正多面体である。すなわち，正四面体，立方体，正八面体，正十二面体，正二十面体であり，プラトンの立体とも呼ぶ。

　すべての面，すべての稜，すべての頂点がそれぞれ区別できない自己交叉多面体は，４種の星型正多面体である。すなわち，小星型十二面体，大星形十二面体，大十二面体，大二十面体である。前二者をケプラーの多面体，後二者をポアンソの多面体と呼ぶこともあり，総称してケプラー・ポアンソの多面体という。

　すべての面，すべての稜，すべての頂点がそれぞれ区別できない複合多面体は，５種の正複合多面体である。これについては前回詳しく見た。

・正複合多面体の芯と星型
　５種類の正複合多面体の凸包は，正四面体×５，正四面体×10，立方体×５の３種は正十二面体であり，正四面体×２は立方体，正八面体×５は二十十二面体になる。それでは，これらの正複合多面体の芯，すなわち正複合多面体を構成する正多面体の共通部分は，どんな形だろうか。
　芯とは，複合多面体や自己交叉多面体において，すべての面によって囲まれる凸多面体のことである。凸包が，複合多面体や自己交叉多面体を内部に含む最小の凸多面体であるのに対し，芯は，複合多面体や自己交叉多面体の内部に含まれる最大の凸多面体ということである。
　この芯となる凸多面体の面をずっと広げていって，他の面と交叉したところを稜とすると，もとの複合多面体，自己交叉多面体が得られる。この操作を「星型化」というのであった。よって正複合多面体は，芯の星型である。すなわち正複合多面体は，星型多面体の一種ということになる。
　星型正多面体においては，小星型十二面体，大星形十二面体，大十二面体の芯が正十二面体，大二十面体の芯が正二十面体であった。正複合多面体の場合はどうだろうか。正四面体からなる正複合多面体から調べていこう。

・正四面体系

　まず，正四面体×５の場合を考える。左の点心図を見ればわかるように，正十二面体に内接する５個の正四面体の正三角形の面は，正十二面体の20個の頂点と，１対１対応している。よって，正十二面体の頂点と面を入れ替えた（すなわち双対な）正二十面体が，これら20枚の正三角形で囲まれる多面体になる。すなわち，正四面体５個からなる正複合多面体の芯は正二十面体である。
　正四面体を一つづつ増やしていって共通部分を求めた様子も下に掲げておく。

　これとまったく同様にして，ケプラーの八角星の芯が，その凸包である立方体の双対，正八面体であることもわかる。
　すなわち，立方体に内接する２個の正四面体の正三角形の面は，立方体の８個の頂点と，１対１対応している。よって，立方体の頂点と面を入れ替えた（すなわち双対な）正八面体が，これら８枚の正三角形で囲まれる多面体になる。

　正四面体10個からなる正複合多面体の芯も正二十面体である。正四面体が５個でも10個でも芯が変わらないのは，正四面体を５個から10個に増やすときに新たに加える面が，すべて既存の面と同一平面上にあるからだ。このことは，正十二面体の点心図を見るとよくわかる。左図における２つの正三角形は，正四面体10個の正複合多面体において，同一平面上にある２つの面の投影像である。

・立方体，正八面体系

　立方体からなる正複合多面体の芯，すなわち５つの立方体の共通部分は，どんな形だろうか。正十二面体の稜心図を見れば，５個の立方体の正方形の面と，正十二面体の30本の稜は，１対１対応している。よって，正十二面体の稜の位置に面があって，30枚の面で囲まれる多面体が芯になることが分かる。もちろんこの多面体は二十面体対称である。

　これは，菱形三十面体に他ならない。正十二面体の各面に正五角錐を乗せて，隣接角錐の斜面を面一にすると，正十二面体の稜の位置に面が来て，菱形三十面体になるのだった。すなわち，立方体５個からなる正複合多面体の芯は菱形三十面体である。
　立方体を一つづつ増やしていって共通部分を求めた様子も下に掲げておく。

　正八面体からなる正複合多面体の芯は正二十面体である。正四面体10個の正複合多面体が，ケプラーの八角星５個の正複合多面体であることを考えると，これは納得がいく。ケプラーの八角星の芯は正八面体であり，正八面体からなる正複合多面体は，「ケプラーの八角星の芯」の正複合多面体ととらえることができるからだ。「ケプラーの八角星の芯」の正複合多面体の芯は，当然ケプラーの八角星の正複合多面体の芯（すなわち正四面体10個の正複合多面体の芯）と一致し，それは正二十面体なのである。

　正八面体からなる正複合多面体では，総計40枚の面のうち２枚づつが同一平面上に来る。そのせいで，正八面体ごとに色を変えるとＣＧがうまく描けないので，芯は単色にしている。実は，５個目の正八面体の面はすべて４個目までの正八面体の面と同一平面上に来るので，正八面体を４個複合させた時点で芯の正二十面体が現れている。
　ちなみに，この芯の正二十面体の頂点は，５個の正八面体の稜を黄金分割している。

・芯と凸包と双対関係
　正八面体からなる正複合多面体は，立方体からなる正複合多面体の双対である。すなわち，両者は頂点と面を入れ替えた関係にある。芯がどんな多面体になるかは，この双対関係からも導くことができる。
　立方体５個の正複合多面体の頂点は，正十二面体の頂点と一致する。この状況で，頂点と面を入れ替えると，正八面体５個の正複合多面体の面中心が，正二十面体の面中心と一致していることがわかる。これはすなわち正八面体からなる正複合多面体の芯が正二十面体であることを意味する。
　また，正八面体５個の正複合多面体の頂点は，二十十二面体の頂点と一致する。この状況で，頂点と面を入れ替えると，立方体５個の正複合多面体の面中心が，菱形三十面体の面中心と一致していることがわかる。これはすなわち立方体からなる正複合多面体の芯が菱形三十面体であることを意味する。
　つまり，双対な複合多面体同士では，凸包と芯が互いに双対な凸多面体になるのである。正四面体からなる３種の正複合多面体は，自己双対であるから，自分の凸包と自分の芯が互いに双対である。
　この関係は，星型正多面体でも同様に成り立つ。小星形十二面体の双対は大十二面体であり，両者の凸包はともに正二十面体，芯はその双対の正十二面体である。大星形十二面体の双対は大二十面体であるが，前者は凸包も芯も正十二面体，後者は凸包も芯も正二十面体である。確かに双対多面体同士で，凸包と芯が互いに双対な多面体になっている。

以上の結果を表にまとめておこう。双対なもの同士を比べると，面数と頂点数が入れ替わっていて，面がもつ頂点数と頂点に集まる面数も入れ替わっているほか，凸包と芯が互いに双対になっている。

形・名称	双対	凸包	芯	面形状	頂点周りの面数	面数	稜数	頂点数
正四面体２個	自己双対	立方体	正八面体	正三角形	3	8	12	8
正四面体５個	自己双対	正十二面体	正二十面体	正三角形	3	20	30	20
正四面体10個	自己双対	正十二面体	正二十面体	正三角形	3	40	60	40
立方体５個	正八面体５個	正十二面体	菱形三十面体	正方形	3	30	60	40
正八面体５個	立方体５個	二十十二面体	正二十面体	正三角形	4	40	60	30
小星形十二面体	大十二面体	正二十面体	正十二面体	正5/2角形	5	12	30	12
大十二面体	小星形十二面体	正二十面体	正十二面体	正五角形	5/2	12	30	12
大星形十二面体	大二十面体	正十二面体	正十二面体	正5/2角形	3	12	30	20
大二十面体	大星形十二面体	正二十面体	正二十面体	正三角形	5/2	20	30	12

2010-11-08

正十二面体から正複合多面体をつくる

正多面体

・正十二面体の内接正多面体
　前回まで三回にわたって，正十二面体の直投影図について見てきた。その中で，適当な補助線を引くと，正十二面体の点心図には正四面体の面心図が現れ，正十二面体の稜心図には立方体の面心図が現れることを見た（下図左，中）。

　正四面体の面心軸は点心軸と一致する*1から，正十二面体の点心図に正四面体の点心図を見いだすこともできる（上図右）。つまり，正十二面体に対して，頂点を共有するように正四面体と立方体を内接させると，正四面体の面心軸（点心軸）は正十二面体の点心軸（の一部）と一致し，立方体の面心軸は正十二面体の稜心軸（の一部）と一致する。

・内接正四面体を重ねる

　つまりこういうことだ。正十二面体の点心軸（三回対称軸）は，正四面体の面心軸（三回対称軸）をすべて含んでいる。正十二面体の点心軸10本のうち，４本を互いに隣り合わないように選ぶと，それは正四面体の面心軸と一致する。正十二面体を固定したとき，このような軸の選び方は５通りある。正四面体では，面心軸に対する面の向きに区別があるから，内接正四面体のとりかたは，この２倍の10通りである。この10個の正四面体をすべて重ねると，二十面体対称な複合多面体になる（右図）。

　正四面体を半数の５個（各軸から１個づつ）重ねても，二十面体対称な複合多面体が得られる（上図）。これはキラルな複合多面体であり，互いに鏡映の関係にある二種が存在する。正四面体５個の複合多面体と，その鏡像を重ねたものが，正四面体10個の複合多面体になっている。
　少しわかりにくいかもしれないので，正四面体を１つづつ増やしていった図を掲げておく。

・内接立方体を重ねる

　正十二面体と内接立方体の関係もこれと似たようなことがいえる。すなわち，正十二面体の稜心軸（二回対称軸）は，立方体の面心軸（四回対称軸）をすべて含んでいる。正十二面体の稜心軸15本のうちから，直交する３本を選ぶと，それが立方体の面心軸になる。このような選び方は５通りあるから，正十二面体を固定したときの内接立方体のとりかたも，５通りある。この５つの立方体をすべて重ねると，二十面体対称な複合多面体になる。この複合多面体は鏡映対称である。
　立方体をひとつづつ増やしていった様子も掲げる。

・複合多面体
　複合多面体とは，広義には，互いに交叉する複数の多面体を，その位置関係を含めて一括してとらえた三次元図形のことである。複合多面体は，面や稜が連結でないから多面体ではない。英語では，「polyhedron compound」とか「polyhedral compound」，すなわち「多面体の複合体」とか「多面複合体」と呼んで，多面体でないことが一応明示されるようだ。ともあれ日本語では「複合多面体」が定訳なので，それをそのまま用いる。

　多面体の複合体が複合多面体とはいえ，ふつうに「複合多面体」というときは，その中でも対称性の高いものに限られる。すなわち正多面体と同じ回転対称性をもつもののみが「複合多面体」とされることが多い。必ずしも同じ多面体を複合させたものに限らない。例えば双対多面体である立方体と正八面体の複合体や，正十二面体と正二十面体の複合体なども複合多面体である。特に，大きさをうまく調節すると，立方体と正八面体からは凸包*2が菱形十二面体となる複合多面体が得られ，正十二面体と正二十面体からは凸包が菱形三十面体となる複合多面体が得られる。
・正複合多面体
　先に挙げた，正十二面体に内接する３種の複合多面体（正四面体10個，正四面体５個，立方体５個）は，複合多面体のなかでも特に対称性が高い。すべての面，すべての稜，すべての頂点がそれぞれ区別できないので，正複合多面体と呼ばれる。正十二面体は，これらの正複合多面体にただ外接するのではなく，これらの正複合多面体の凸包になっている。

　正複合多面体には，これらのほかにケプラーの八角星と，５つの正八面体の複合多面体があって，合計５種である。ケプラーの八角星は，立方体に内接する二つの正四面体からなる正複合多面体で，八面体対称である。ダビデの星（正6/2角形）の三次元バージョンともいえる。正十二面体に内接する10個の正四面体のうち，鏡映の位置にある２つを合わせた複合多面体といえる。
　立方体５個からなる正複合多面体において，立方体を，それに内接する正四面体でうまく置き換えると，正四面体５個からなる正複合多面体が得られ，ケプラーの八角星で置き換えると，正四面体10個からなる正複合多面体が得られる。

　立方体を，それと双対な正八面体で置き換える（左図）と，正八面体５個からなる正複合多面体が得られる。これの凸包はどんな形かわかるだろうか？正八面体の頂点の位置は，正十二面体の内接立方体の面の中心，すなわち正十二面体の稜の中心の位置にある*3。よって，凸包の形状は，正十二面体の稜中点をつないでできる準正多面体*4，二十十二面体である。

　二十十二面体は，正十二面体（又は正二十面体）を，稜の中点まで切頂して得られる準正多面体である。二十十二面体の30個の頂点のうち，対向頂点を３組，各組を結ぶ直線が互いに直交するように選ぶと正八面体ができる。このような選び方には５通りがあり，この５つの正八面体の複合体が５つ目の正複合多面体になるのである。

*1:正四面体の中心と面の中心を通る軸（面心軸）は頂点も通るから点心軸でもある。正四面体では，面心図と点心図は，裏から見たか表から見たかの違いである。

*2:非凸多面体や複合多面体の凸包とは，それをすっぽり包む最小の凸多面体のこと。非凸多面体や複合多面体の隣接頂点をつないでできる凸多面体が凸包になる。

*3:立方体と正八面体は双対であるから頂点と面中心は互いに同じ位置にある。内接立方体に屋根をかぶせて正十二面体にするとき，屋根頂上の稜線は正十二面体の稜であり立方体の面中心の真上にある。

*4:すべての稜とすべての頂点がそれぞれ区別のつかない多面体。

2010-10-26

正十二面体と黄金比（その３：点心図から）

正多面体投影図黄金比

・正十二面体の点心直投影
　正十二面体の対向する頂点の中心をつなぐ直線は，三回対称軸である。すなわち，この軸まわりに，360°/3＝120°回転させると正十二面体は回転前と完全に一致する。よって，この軸に平行な光線で直投影をおこなうと，その投影図は三回対称性をもつ。正十二面体は全部で20個の頂点をもち，対向頂点の組は10組ある。よって，三回対称軸も10本あり，当然ながら光線をどの三回対称軸に平行にしても，同じ点心図が得られる。

　正十二面体の直投影による点心図では，３つの合同な五角形が中心を囲んでおり，その外側にまた３つの合同な五角形がある。輪郭は正六角形を切頂した準正十二角形である。この準正十二角形の長いほうの辺は，スクリーンと平行な稜が直投影されたものなので，長さが稜長と等しい。正十二面体の稜長を１とすると，この点心図には，長さ $\phi$ の辺をもつ正三角形（水色）と，長さ１の辺と $\phi$ の辺を交互にもつ準正六角形（赤）が隠れている*1。

・正十二面体に内接する正四面体

　この準正六角形の頂点を一つおきにつないで得られる正三角形は，正十二面体と頂点を共有する正四面体の面心直投影になっている。正十二面体の頂点を一つおきに選ぶと，（頂点を共有しつつ）内接する立方体が得られたように，頂点を二つおきに選ぶと，内接する正四面体が得られるのだ（右図）。準正六角形の中心を通らない対角線の長さは，余弦定理により， $\sqrt{1+\phi^2-2\phi\cos{\frac{2\pi}{3}}}=\sqrt{1+\phi^2+\phi}=\sqrt{2}\phi$ 。
　つまり，稜長１の正十二面体に内接する正四面体の稜長は $\sqrt{2}\phi$ である。一方，前回稜心図で見たように，内接する立方体の稜長は $\phi$ である。正十二面体に内接する立方体の頂点を一つおきにつなぐと内接四面体が得られるから，この関係は当然と言えば当然だ。

・正十二面体の頂点間距離
　今までの結果から，正十二面体の頂点間距離がすべて分かる。それを近い順に並べると， $1,\phi,\sqrt{2}\phi,\phi^2,\sqrt{3}\phi$ (1,1.618,2.288,2.618,2.803)となり，黄金比がきれいに現れる。対向頂点間距離 $\sqrt{3}\phi$ は内接立方体の対向頂点間距離でもあるのですぐ出るし，その直前の $\phi^2$ は正十二面体の稜接球の直径と一致することから算出できる。

　点心図には，このうち $\sqrt{3}\phi$ を除く頂点間距離が現れている（赤，水色，緑，橙の順）。また，稜心図には，すべての頂点間距離が出現する（赤，水色，緑，橙，紫の順）。面心図には $\sqrt{2}\phi$ と $\sqrt{3}\phi$ を除く頂点間距離が現れる（赤，水色，橙の順）。
　下図のように，１つの頂点から隣接頂点へ向かって，正十二面体を次々に切り開くと，その断面に，これらの頂点間距離を辺長とする三角形の系列が得られる。

・点心図の寸法
　ほかの部分の寸法は，次のようになる。

　まず，中央寄りの五角形は，長さ $\phi$ の対角線から図の中心にある頂点までの高さが，辺長 $\phi$ の正三角形 $ABC$ の内接円の半径に等しく， $OJ=\frac{\sqrt{3}\phi}{6}\simeq0.467$ である。ここで，正三角形の内接円半径が高さの1/3であることを用いた。よって，全体の高さは $OK=\frac{(1+\phi)\sqrt{3}\phi}{6}=\frac{\phi^3\sqrt{3}}{6}\simeq1.223$ 。
　外側の五角形は，もっとつぶれていて，その高さは，中央寄りの五角形の高さ $OK$ から，正三角形の外接円の半径 $OA$ を引いた値になる。正三角形の外接円半径はその高さの2/3（内接円半径の２倍）であるから，外側五角形の高さは， $BM=\frac{\phi^3\sqrt{3}}{6}-\frac{\sqrt{3}\phi}{3}=\frac{\phi\sqrt{3}(\phi^2-2)}{6}=\frac{\sqrt{3}}{6}\simeq0.289$ である。
　よって，これら二種の五角形の高さの比（＝面積比）は，黄金比の三乗 $\phi^3\simeq4.236$ であることがわかる。さらに，これらの五角形の高さが，対角線によって黄金分割されることを考えると，
$BL:LM:BM:OJ:JK:OK=1:\phi:\phi^2:\phi^3:\phi^4:\phi^5$ 　となって，黄金比がたくさん出てくる。

・輪郭と投影面積
　輪郭の準正十二角形の面積を求めてみよう。点心図において，大きい方の五角形は，高さが $\frac{\phi^3\sqrt{3}}{6}$ で，もとの正五角形の高さが $\frac{(\phi+2)}{2\sqrt{3-\phi}}$ だから，その $\frac{\phi^3\sqrt{3(3-\phi)}}{3(\phi+2)}$ 倍である。小さい方はこの $\frac{1}{\phi^3}$ 倍である。
　よって，６つの五角形の面積を合計すると，正五角形の面積の $\frac{(1+\phi^3)\sqrt{3(3-\phi)}}{\phi+2}=\frac{2\phi^2\sqrt{3(3-\phi)}}{\phi+2}\simeq2.947$ 倍である。この面積は，稜心直投影の輪郭より大きく，面心直投影の輪郭より小さい。直投影の輪郭面積と正五角形の面積の比は，稜心，点心，面心の順に，
$\frac{2\phi^3\sqrt{3-\phi}}{\phi+2}\simeq2.753$ ， $\frac{2\phi^2\sqrt{3(3-\phi)}}{\phi+2}\simeq2.947$ ， $2\phi\simeq3.236$ ，となる。
　輪郭の準正十二角形の外接円半径は，準正六角形のそれと等しく， $\sqrt{(\frac{\phi^3\sqrt{3}}{6})^2+(\frac{1}{2})^2}=\frac{\sqrt{6}\phi}{3}\simeq1.321$ 。これは，稜心図の輪郭（平行六辺形）の外接円半径 $\frac{\sqrt{3}\phi}{2}\simeq1.401$ や，面心図の輪郭（正十角形）の外接円半径 $\frac{\phi}{\sqrt{3-\phi}}\simeq1.376$ よりも小さい*2。

　輪郭の準正十二角形の長さ１の辺を延長すると正六角形が得られる（右図左）が，その辺長は，中央寄りの五角形の高さを高さとする正三角形の辺長と一致する。このことは正六角形に中心を通る対角線を引くとすぐわかる。よって，正六角形の辺長は， $\frac{\phi^3\sqrt{3}}{6}$ を $\frac{\sqrt{3}}{2}$ で割って， $\frac{\phi^3}{3}\simeq1.412$ となる*3。この正六角形の各頂点を，辺の長さにして $\frac{\frac{\phi^3}{3}-1}{2}=\frac{1}{3\phi}$ だけ切頂したものが，輪郭の準正十二角形になるから，準正十二角形の１でない辺長は， $\frac{1}{\sqrt{3}\phi}\simeq0.206$ である*4。この辺の中心からの距離は， $\frac{\phi^3}{3}-\frac{1}{6\phi}=\frac{2\phi^4-1}{6\phi}=\frac{\phi^2}{2}$ であり，もしこれを延長すると，先ほどよりもやや大きな，辺長 $\frac{\phi^2}{\sqrt{3}}\simeq1.512$ の正六角形が得られる（図右）。

・二面角
　点心図に現れる二種の五角形の寸法からも，正十二面体の二面角 $\delta$ を求めることができる。
　手前の大きな五角形に投影される面がスクリーンとなす角 $\theta_1$ と，裏側の小さな五角形に投影される面がスクリーンとなす角 $\theta_2$ の和が $\delta$ になる。上で見たように，点心図において，大きな五角形，小さな五角形は，正五角形を対称軸の方
向に，それぞれ $\frac{\phi^3\sqrt{3(3-\phi)}}{3(\phi+2)}$ 倍， $\frac{\sqrt{3(3-\phi)}}{3(\phi+2)}$ 倍に縮小したものであるから，
　 $\cos{\theta_1}=\frac{\phi^3\sqrt{3(3-\phi)}}{3(\phi+2)}$
　 $\cos{\theta_2}=\frac{\sqrt{3(3-\phi)}}{3(\phi+2)}$
　であり，これを解くと， $\theta_1\simeq$ 37.38°， $\theta_2\simeq$ 79.19°となり，二面角 $\delta$ は約116.6°となる。

*1:直投影が平行な線分の長さの比を保つことと，正五角形の辺と対角線の長さの比が $\phi$ であることから，正十二面体の直投影に現れる五角形の，平行な辺と対角線の長さの比も $\phi$ であることがわかる。

*2:稜心図輪郭の外接円は外接球の投影だから，稜長１の正十二面体をどのように直投影しても，半径 $\frac{\sqrt{3}\phi}{2}\simeq1.401$ の円の中に収まる。逆に，稜心図輪郭の内接円は内接球の投影だから，稜長１の正十二面体をどのように直投影しても，輪郭には半径 $\frac{\phi^3}{2\sqrt{\phi+2}}\simeq1.114$ の円が収まる。実際，点心図の輪郭の内接円半径は，大きめの五角形の高さ $\frac{\phi^3\sqrt{3}}{6}\simeq1.223$ である。

*3:辺長１の正三角形の高さは， $\cos{\frac{\pi}{6}}=\frac{\sqrt{3}}{2}$ である。

*4:切頂によって除かれる三角形は，等辺の長さが $\frac{\sqrt{3}}{2}$ で，底角が30°の二等辺三角形だから，底辺の長さは $2\frac{\sqrt{3}}{2}\cos{\frac{\pi}{6}}=\frac{1}{\sqrt{3}\phi}$ 。

2010-10-19

正十二面体と黄金比（その２：稜心図から）

正多面体黄金比投影図

・正十二面体の稜心直投影
　正十二面体の対向する稜の中心をつなぐ直線は，その稜に垂直で，二回対称軸である。すなわち，この軸周りに，360°/2＝180°回転させると正十二面体は回転前と完全に一致する。よって，この軸に平行な光線で直投影をおこなうと，その投影図も二回対称性をもつ。正十二面体は全部で30本の稜をもつから，対向稜の組は15組ある。よって，二回対称軸も15本あり，当然ながら光線をどの二回対称軸に平行にしても，同じ稜心図が得られる。

　しかも，15本の二回対称軸は，互いに直交する３本を１組とする５組に分けられる。この５組の３直交軸は，正十二面体の稜の向きとも一致する。正十二面体の１つの面は，垂直でも平行でもない５本の稜に囲まれているが，全30本のどの稜も，この５稜のいづれかに平行又は垂直である。左図では，５組の稜を組ごとに色分けしている。
　具体的には，稜の属する面における，その稜と対向する頂点を端にもち，かつその面上にない稜は，もとの稜と互いに垂直であり，互いに対向する稜は互いに垂直である。言い換えると，稜長１の正十二面体において，稜に沿って測った最短距離が，２である稜同士は垂直であり，５である稜同士は平行である。

　互いに垂直な３枚の直投影を組み合わせて，正面図，平面図，側面図としたものを正投影という。正十二面体では，この３枚の直投影の光線を同時に二回対称軸に平行に配置することができる。つまり，正十二面体の正投影において，正面図，平面図，側面図をいづれも稜心図にすることができる（左図）。

・稜心図の形状

　直投影による正十二面体の稜心図では，中央に１本の線分があり，これはもとの正十二面体の稜と合同である。よってこの稜長を１とすると，稜心図中央の線分の長さも１である。このほかに，輪郭を構成する２本の平行な線分も稜と合同で長さ１になる。これを左図では赤線で示した。正十二面体上でこれらの稜と垂直なもう２本の稜は，稜心図では輪郭の一点に退化している。図における左右の頂点がそれである。
　この輪郭は六角形である。なぜなら，光線に平行なため一点に退化する稜（２本）を含む面（４枚）は，当然光線に平行で，投影図では線分に退化するからである。それが輪郭を構成する斜めの線分になる。よって，正十二面体の稜心図では，面は４枚しか見えない。これらの裏側にもまったく同じ配置の４面があるから，隠線処理の有無によって稜心図は変化しない。
　直投影は，平行な線分の長さの比を保つから，稜心図における各五角形において，赤色の辺に平行な水色の対角線は長さが $\phi$ である*1。よって，この４本の対角線は正方形をつくる。あとで見るように，輪郭の六角形は，黄金菱形*2を切頂した平行六辺形*3である。

・稜心図の寸法
　稜心図で見えている４枚の五角形は，どれも長さ１の辺をもつ。この正方形は，一部の頂点を共有しつつ正十二面体に内接する立方体の面心直投影にほかならない。稜長 $\phi$ の立方体の各面に屋根をとりつけて，稜長１の正十二面体を得ることができるが，これはそのことに対応する。

　稜心図に出てくる寸法を，もう少し詳しく見ていこう。
　まず，中央の線分を含む五角形は，対角線までの高さが正方形の辺長の半分に等しく， $OH=\frac{\phi}{2}$ 。全体の高さはこの $(1+\frac{1}{\phi})=\phi$ 倍*4で， $OE=\frac{\phi^2}{2}$ 。
　残りのやや小ぶりの五角形は，対角線と頂点の距離が $KG=\frac{AB-GF}{2}=\frac{\phi-1}{2}=\frac{1}{2\phi}$ であるから，全体の高さはこの $(1+\phi)=\phi^2$ 倍で， $GL=\frac{\phi}{2}$ 。よって，これら２種の五角形の高さの比は黄金比であることがわかる。
　また，輪郭の平行六辺形の高さと幅は等しく， $2OL=2OE=\phi^2$ である。立方体の各面に合同な屋根をつけたのが正十二面体であるから，そうでなくてはならない。屋根の高さは $KL=HE=\frac{1}{2}$ である。
　△EABは，底辺が $\phi$ ，高さが $\frac{1}{2}$ の二等辺三角形であるから，黄金菱形を長対角線で二等分したものである。したがって，正十二面体の稜心直投影の輪郭は，黄金菱形の鋭角を切頂した平行六辺形であることがわかる。この黄金菱形は，短対角線の長さが $\phi^2$ ，長対角線の長さが $\phi^3$ であり，輪郭の平行六辺形は，この鋭角を $\frac{1}{\phi^2}$ だけ切頂したものである。さらに深く，鋭角を $\frac{1}{\phi}$ 切頂し，鈍角を $\frac{1}{\phi^2}$ 切頂すると，水色の正方形が得られる。

・投影面積と二面角
　輪郭の平行六辺形の面積を求めてみよう。稜心図において，大ぶりな五角形は高さが $\frac{\phi^2}{2}$ で，もとの正五角形の高さ*5が $\frac{\phi+2}{2\sqrt{3-\phi}}$ だから， $\frac{\phi^2\sqrt{3-\phi}}{\phi+2}$ 倍である。小ぶりな五角形はこの $\frac{1}{\phi}$ 倍である。
　よって，４つの五角形の面積の合計は，正十二面体の１つの面の面積の $\frac{2\phi^3\sqrt{3-\phi}}{\phi+2}\simeq2.753$ 倍である*6。

　前回は，面心直投影から正十二面体の二面角を算出したが，稜心直投影からも二面角を求めることができる。
　稜心図で中央の線分を含む五角形に投影される面が，スクリーンとなす角は，対称性から二面角δの補角の半分である。この五角形の縮小率は， $\frac{\phi^2\sqrt{3-\phi}}{\phi+2}$ であるから，前回と同様にして，
$\cos{\frac{\pi-\delta}{2}}=\frac{\phi^2\sqrt{3-\phi}}{\phi+2}$
　これを解くと，二面角δはやはり約116.6°となる。

・稜心図と三接球

　稜心直投影の寸法から，内接球，稜接球，外接球の大きさが求められる。
　最も簡単なのは，稜接球の半径であり， $r_m=OR=OS=\frac{\phi^2}{2}\simeq1.309$ となる。
　次に，外接球の半径は， $r_o=OP=\sqrt{OS^2+SP^2}=\frac{\sqrt{\phi^4+1}}{2}=\frac{\sqrt{3}\phi}{2}\simeq1.401$ 。
　そして，△OQRが黄金菱形を対角線で四等分した直角三角形であることに注意すると，内接球の半径は，
$r_i=OQ=\frac{\phi}{\sqrt{\phi^2+1}}OR=\frac{\phi^3}{2\sqrt{\phi+2}}\simeq1.114$ 。
　最後に，三接球と稜心直投影の関係を図に示しておこう。

*1:この対角線は，もとの正十二面体を構成する正五角形の，スクリーンに平行な対角線の直投影だから，投影前と等長である。

*2:対角線の長さの比が黄金比 $\phi$ である菱形。

*3:対向する辺が平行で等長な六角形。

*4:正十二面体の直投影に現れる五角形において，一本の対角線は，その対角線に関する高さを黄金分割する。

*5:前回の計算結果を用いた。

*6:正十二面体を直投影したときに，その輪郭が囲む面積のうちで，最も小さいのがこの平行六辺形の面積と思われるが，あっているだろうか？

2010-10-14

正十二面体と黄金比（その１：面心図から）

正多面体黄金比投影図

・正十二面体の直投影
　先月の記事で，黄金比と正五角形の関係について述べた。その正五角形からなる正多面体である正十二面体も，黄金比と密接な関係がある。今回から三回かけて，正十二面体の直投影を通して，正十二面体と黄金比の関係について触れてみたい。
　多面体の直投影については，前々回ざっと説明したが，大事なことを確認しておく。
　直投影とは，平行光線による，それと垂直なスクリーンへの投影である。よって，多面体上の，スクリーンに平行な多角形や線分は，それと合同な多角形や線分に投影される。多面体上の，互いに平行な線分は，互いに平行な線分に投影され，しかもそれらの線分の長さの比は等しい。つまり平行性と長さの比は保たれる。線分上に内分点があれば，それを直投影しても，内分比は変わらない。
　正十二面体は正五角形の面のみで構成されている。よって，正十二面体の直投影は，正五角形を直投影した五角形のみで構成される。一般の配置では，正十二面体の面はスクリーンと平行でないため，直投影の五角形は正五角形ではない。正五角形ではないが，正五角形と同様に黄金比を多くもつ五角形である。

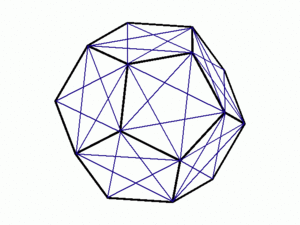
　このことは，直投影が平行線分の長さの比を変えないことからわかる。この五角形の各辺には，それぞれ平行な対角線がある。平行な辺と対角線の長さの比は黄金比 $\phi$ である。また，各々の対角線は，他の対角線を黄金分割する。一本の対角線は，五角形の高さを黄金分割し，五角形の面積を黄金二乗分割する。さらに，対角線を引いてできる三角形*1の面積は５種類あり，それらを順に並べると隣合う面積の比は黄金比 $\phi$ になっている。

・正十二面体の面心直投影
　正十二面体の対向面の中心をつなぐ直線は，五回対称軸である。すなわち，この軸まわりに，360°/5＝72°回転させると正十二面体は回転前と完全に一致する。よって，この軸に平行な光線で直投影をおこなうと，その投影図は五回対称性をもつ。
　中心に一つの正五角形面があり，これはもとの正十二面体の面と合同である。よって正十二面体の稜長を１とすると，投影図の中央の正五角形の辺長も１である。これを下方の図では赤線で示した。

　この正五角形の各頂点から放射状に線分が伸び，それらの先端が少し大きな正五角形（水色）の頂点の位置に来る。そしてここから二本づつ線分が伸びて，投影図の輪郭は正十角形になっている。輪郭が正十角形になる理由は，対称性からというだけで充分であろう。隠線を描けば一目瞭然だ（右図）。

・面心直投影図の寸法
　正十二面体の面心図では，面は中心に１枚，周囲に５枚の計６枚見えている。正十角形の大きさはどれくらいだろうか？これは簡単に求めることができる。先の大きな正五角形に注目すると，これは中心の正五角形と相似比が黄金比 $\phi$ になっている。なぜなら，大きな正五角形の辺は，周辺５枚の五角形の対角線であり，この対角線（水色）の長さはこれと平行な辺（赤）の長さの $\phi$ 倍だからである。これさえわかれば，作図が可能になる。

　寸法をいくつか求めておこう。まず， $AB=1$ ， $CE=\phi\simeq1.618$
$OA=\frac{GA}{\sin{\frac{\pi}{5}}}=\frac{\frac{1}{2}}{\sin{\frac{\pi}{5}}}=\frac{1}{\sqrt{3-\phi}}\simeq0.851$
$OE=OD={\phi}OA=\frac{\phi}{\sqrt{3-\phi}}\simeq1.376$
$OG=\frac{GA}{\tan{\frac{\pi}{5}}}=\frac{\frac{1}{2}}{\tan{\frac{\pi}{5}}}=\frac{\phi}{2\sqrt{3-\phi}}\simeq0.688$
　上２式から，GはODの中点であるから，ABとODはGにおいて互いを垂直二等分する。よって，△AODは底角36°の二等辺三角形。すると，△DAEは△ODEと相似な黄金三角形*2であることがわかり，二等辺三角形であるから，DE=DA=OA。つまり，輪郭の正十角形の辺長は，中央の正五角形の外接円半径と一致する。
　次に黄色の線に着目して，周辺の五角形がどの程度つぶれているかを調べる。
$GH=GO+OH=GO+OA=GO+\frac{2}{\phi}GO=(1+2\phi-2)GO=(2\phi-1)GO$
GO=GDであったから，中央の正五角形と周辺の五角形は，底辺を共有して高さの比が $(2\phi-1):1=$ 約2.236:1になっている。当然，面積比も $(2\phi-1):1$ で，輪郭の正十角形の面積*3は，中央の正五角形の $1+\frac{5}{2\phi-1}=2\phi=$ 約3.236倍である。

・二面角の算出
　面心図に現れる二種の五角形の寸法から，正十二面体の二面角δを求めることができる。
　中心の正五角形に投影される面は光線と垂直，スクリーンと平行であり，周辺のつぶれた五角形に投影される面がスクリーンとなす角はδの補角である。そして面がスクリーンとなす角は，その法線が光線となす角と等しく，これをθとすると，その面の直投影はもとの面を一方向にcosθだけ縮小した形になる。そしてすぐ上で見たように，面心図において，つぶれた五角形は正五角形を対称軸の方向に $(2\phi-1)$ 分の1に縮小したものであるから，
$\cos(\pi-\delta)=2\phi-1=\sqrt{5}$ 　であり，これを解くと，二面角δは約116.6°となる。

・正十角形からの作図
　正十二面体の面心直投影は，正十角形から次のようにして簡単に作図できる。

１．正十角形に，頂点を二つおきにつなぐ対角線を描く。対角線は星型正十角形*4になる。
２．対角線の芯にできる正十角形の頂点を一つおきにつないで，正五角形を描く。
３．正五角形の頂点と輪郭の正十角形の頂点を，放射状につなぐ。
４．隠線もまったく同様にして得られる。

*1:一般には合同なものはない

*2:頂角36°の二等辺三角形

*3:正十二面体を直投影したときに，その輪郭が囲む面積のうちで，最も大きいのがこの正十角形の面積と思われるが，あっているだろうか？

*4:正10/3角形